From
\[\frac{1}{x}-\frac{2}{a}+\frac{3}{x+a}=0\]
We get:
\[2x^2-2ax-a^2=0\Rightarrow x = \frac{1}{2}a+\frac{\sqrt{3}}{2}a = a\cos 30^{\circ} + a \sin 30^{\circ}\]
View attachment 7019
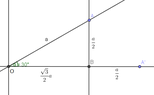
Construction of $x$: Divide a right angle (in the 1st quadrant) into three equal angles. This is done in three small steps with a compass. Let segment $a$ ($|OA|$) be the hypotenuse with an angle of 30 degrees to the horizontal line. From point $A$ draw a vertical line to meet the $x$-axis in point $B$. The adjacent catheter of triangle $OAB$ has the length: $\frac{\sqrt{3}}{2}a$, whereas the opposing catheter has the length $\frac{1}{2}a$. Now, add a half segment $a$ to the adjacent catheter (point $A’$). Our $x$ is then |OA’|.
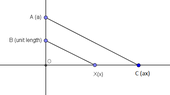
View attachment 7020Construction of $ax$: Mark segment $a$ on the $y$-axis (from Origo, point $A$). Mark segment $x$ on the $x$-axis (from Origo, point $X$). Then mark the unit length (point $B$) on the $y$-axis. Now connect $B$ and $X$. Draw a line through point $A$ parallel to the line through $B$ and $X$. The line cuts the $x$-axis in point $C$ at a distance $ax$ from Origo. This is easily seen from the two triangles (with equal angles):
$\frac{|OX|}{|OB|} = \frac{|OC|}{|OA|} \rightarrow \frac{x}{1}=\frac{|OC|}{a} \rightarrow |OC| = ax$.
View attachment 7021
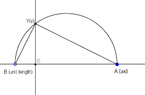
Construction of $y = \sqrt{ax}$:
Mark segment $ax$ on the $x$-axis (point $A$). Then mark the point of unit length starting from Origo to the left (point $B$). Draw the half circle with diameter $|AB|$. The half circle and the $y$-axis cross in point ($Y$). We have two triangles with equal angles: OAY and OBY. Thus, we have the relation:
\[\frac{|Y|}{1} = \frac{|OA|}{|Y|}\rightarrow |Y|^2 = |OA| \rightarrow |Y| = \sqrt{|OA|}\rightarrow y = \sqrt{ax}\]