nacho-man
- 166
- 0
Hey just needed some help working with this.
I can't find any relevant textbooks and the lecture slides i have a very vague to go off from.
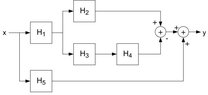
I've attached an image, and this my attempt.
I'd like to add, in my notes the lecturer used an example feedback loop and had an error signal.
I am not sure if that would always be included or not? I have no idea what branch mathematics this falls under, what it is for etc so it's been really hard for me to read up on. if anyone could give me guidance in regards to these issues that would also be greatly appreciated.
anyway so ill skip ahead to my attempt at this question.
the output we are looking for is $Y(Z)$
I split the inputs into 3 components,
letting
$Y_1(Z)$ = $H_2(Z)H_1(Z)$
$Y_2(Z)$ = $H_4(Z)H_3(Z)H_1(Z)$
$Y_3(Z)$ = $H_5(Z)$
$Y(Z) = Y_3(Z) + Y_1(Z) - Y_2(Z)$
which i would just expand and simplify from there?
Is this correct, I am quite lost on this topic.
any help is greatly appreciated.
I can't find any relevant textbooks and the lecture slides i have a very vague to go off from.
I've attached an image, and this my attempt.
I'd like to add, in my notes the lecturer used an example feedback loop and had an error signal.
I am not sure if that would always be included or not? I have no idea what branch mathematics this falls under, what it is for etc so it's been really hard for me to read up on. if anyone could give me guidance in regards to these issues that would also be greatly appreciated.
anyway so ill skip ahead to my attempt at this question.
the output we are looking for is $Y(Z)$
I split the inputs into 3 components,
letting
$Y_1(Z)$ = $H_2(Z)H_1(Z)$
$Y_2(Z)$ = $H_4(Z)H_3(Z)H_1(Z)$
$Y_3(Z)$ = $H_5(Z)$
$Y(Z) = Y_3(Z) + Y_1(Z) - Y_2(Z)$
which i would just expand and simplify from there?
Is this correct, I am quite lost on this topic.
any help is greatly appreciated.