LLT71
- 73
- 5
so, continuous signals as sums of weighted delta functions can be represented like this:
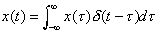
if you switch order of some variables you get ∫x(τ)δ(-τ+t)dτ, and since,I presume, Dirac delta "function" is even I can write it like this ∫x(τ)δ(-(-τ+t))dτ=∫x(τ)δ(τ-t)dτ=x(t) and we got ourselves a "sifting property". can we visualize it like this:
x(τ) is function in "τ domain". for every τ there is x(τ) such that every x(τ) value represents some function x(t) which can be "extracted" using δ(τ-t) or, generally speaking, function x(τ) in τ domain represents some "family of functions" x(t) and by using sifting property, described earlier, we can sift one particular function x(t) from that family?
if this is right, can described sifting property be some kind of "transformation" like Laplace one (you go from one to domain to another, do some things, and go back to original domain)?
thanks!
if you switch order of some variables you get ∫x(τ)δ(-τ+t)dτ, and since,I presume, Dirac delta "function" is even I can write it like this ∫x(τ)δ(-(-τ+t))dτ=∫x(τ)δ(τ-t)dτ=x(t) and we got ourselves a "sifting property". can we visualize it like this:
x(τ) is function in "τ domain". for every τ there is x(τ) such that every x(τ) value represents some function x(t) which can be "extracted" using δ(τ-t) or, generally speaking, function x(τ) in τ domain represents some "family of functions" x(t) and by using sifting property, described earlier, we can sift one particular function x(t) from that family?
if this is right, can described sifting property be some kind of "transformation" like Laplace one (you go from one to domain to another, do some things, and go back to original domain)?
thanks!