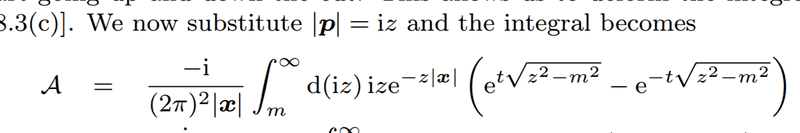Discussion Overview
The discussion revolves around understanding a contour integral example from "QFT for the Gifted Amateur," specifically focusing on the manipulation of integrals and the implications of changing limits of integration. Participants explore the mathematical steps involved in transforming the integral and the reasoning behind these transformations.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant seeks clarification on how a specific integral transforms, referencing a page in the book.
- Another participant explains that the extra exponential term arises from splitting the integral into two parts, one from ##-\infty## to ##0## and another from ##0## to ##\infty##.
- Several participants express confusion about the transformations and substitutions, particularly regarding the limits of integration and the implications of changing variables.
- One participant suggests that exchanging limits of integration typically introduces a minus sign, questioning the validity of the substitution of ##|p|## with ##-|p|##.
- Another participant proposes a mathematical identity involving the integral from ##-\infty## to ##0## and its relationship to the integral from ##0## to ##\infty##, suggesting a possible resolution to the confusion.
Areas of Agreement / Disagreement
Participants express varying levels of understanding regarding the transformations of the integral, with some agreeing on certain mathematical manipulations while others remain uncertain or contest the reasoning behind them. No consensus is reached on the validity of the substitutions and transformations discussed.
Contextual Notes
Participants highlight potential limitations in understanding the implications of changing integration limits and the assumptions underlying the substitutions made in the integral manipulations.
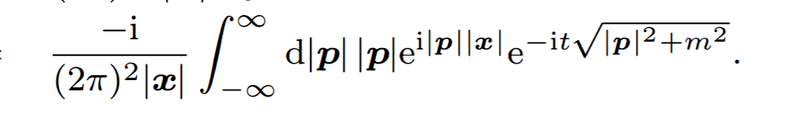 becomes
becomes