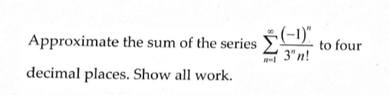Convergence of a Series: Is My Approximation Accurate Enough?

  • MHB
  • Thread starter ardentmed
  • Start date
  • Tags
    Series Sum
In summary, the speaker wanted to confirm their answer to a series question and asked for someone to review their calculations. They concluded that their approximation, Sn, was approximately -0.2835 after reaching the same digits of accuracy with terms S5 and S6. The response was that their calculations were enough to confirm their answer.
  • #1
ardentmed
158
0
Hey guys,

I just wanted to run a quick series question by you guys just to confirm my answer. I'm doubting whether or not I should keep going or if S6 is enough.

View attachment 2804

I got S5 = -0.28347 and S6 = -0.28347, so that is where I concluded than Sn ~ -0.2835.

I would appreciate it if someone could look over this for me and tell me how I did.

Thanks in advance.
 

Attachments

  • sum.PNG
    sum.PNG
    7.9 KB · Views: 55
Physics news on Phys.org
  • #2
ardentmed said:
Hey guys,

I just wanted to run a quick series question by you guys just to confirm my answer. I'm doubting whether or not I should keep going or if S6 is enough.

https://www.physicsforums.com/attachments/2804

I got S5 = -0.28347 and S6 = -0.28347, so that is where I concluded than Sn ~ -0.2835.

I would appreciate it if someone could look over this for me and tell me how I did.

Thanks in advance.

When you get the sum giving you the same digits up to your level of accuracy when you add more terms, then you have reached your approximation. So yes, what you have done is enough.
 

FAQ: Convergence of a Series: Is My Approximation Accurate Enough?

What is a "Sum of a Series" question?

A "Sum of a Series" question is a type of mathematical problem that involves finding the sum of a sequence of numbers. The sequence can be finite or infinite, and the numbers can follow a specific pattern or be randomly generated.

How do you solve a "Sum of a Series" question?

To solve a "Sum of a Series" question, you can use various mathematical methods such as the arithmetic mean, geometric mean, or the formula for finding the sum of a finite geometric series. You can also use a calculator or computer program to find the sum.

What is the purpose of "Sum of a Series" questions?

The purpose of "Sum of a Series" questions is to exercise your mathematical skills and problem-solving abilities. These types of questions are commonly used in education to test students' understanding of mathematical concepts and their ability to apply them in real-world situations.

What are some real-life applications of "Sum of a Series" questions?

"Sum of a Series" questions can be applied in various fields such as finance, physics, and computer science. For example, calculating the sum of a series can help in predicting future financial trends, determining the total distance traveled by an object in physics, or optimizing algorithms in computer science.

Are there any common mistakes when solving "Sum of a Series" questions?

Yes, some common mistakes when solving "Sum of a Series" questions include forgetting to use the correct formula, misinterpreting the given series, or making calculation errors. It is important to carefully read and understand the question and double-check your calculations to avoid these mistakes.

Similar threads

MHB Sum of Infinite Series: Find 1/sqrt(2)
Replies
2
Views
2K
MHB Series Convergence and Divergence I
Replies
11
Views
3K
MHB Series Convergence and Divergence II
Replies
1
Views
1K
Studying the convergence of a series with an arctangent of a partial sum
Replies
7
Views
1K
Infinite series as the limit of its sequence of partial sums
Replies
3
Views
2K
MHB Power Series Problem: Solve f(3x) = 1/(1 - 3x)
Replies
2
Views
1K
MHB Convergence of Series with Square Roots
Replies
8
Views
2K
How to Calculate Error in Fourier Series and its Approximation of Angles?
Replies
1
Views
1K
MHB Series Convergence and Divergence III
Replies
2
Views
1K
MHB Series Convergence Test Questions
Replies
11
Views
3K

Hot Threads

Recent Insights

Back
Top