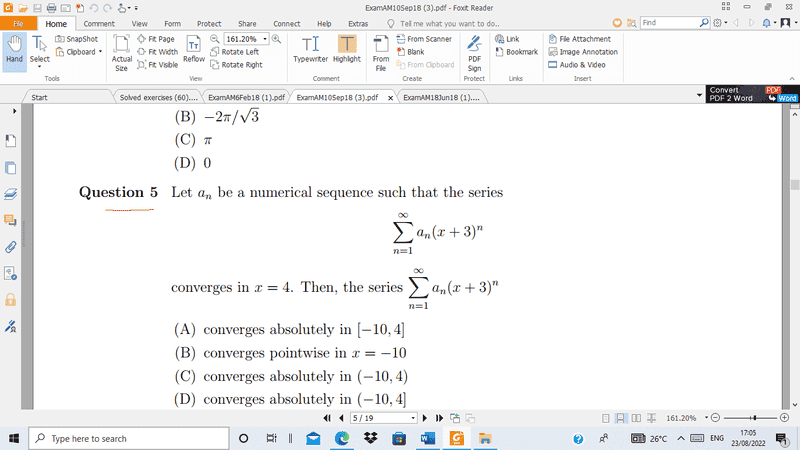Homework Help Overview
The discussion revolves around the convergence of a series and the interpretation of its radius and endpoints. Participants are examining the implications of a statement regarding convergence at a specific point, x=4, and how it relates to the series defined by the transformation y=x+3.
Discussion Character
- Conceptual clarification, Assumption checking, Problem interpretation
Approaches and Questions Raised
- Participants are exploring the relationship between the convergence of the series and the transformation of variables. There is confusion regarding the phrasing of "converges in x=4" and its implications for the radius of convergence and the set of convergence.
Discussion Status
Multiple interpretations of the convergence statement are being explored, with some participants questioning the correctness of the original phrasing. Guidance has been offered regarding the distinction between convergence at a point versus the radius of convergence, but no consensus has been reached on the correct interpretation.
Contextual Notes
There is an ongoing debate about the terminology used in the problem statement, particularly the phrase "converges in x=4," which some participants find misleading. The distinction between the radius of convergence and the set of convergence is also under scrutiny.