Convert infinite solution to vector form

[ibwev]

View attachment 4013
View attachment 4014

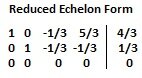
I know the solution has an infinite number of solutions. It is represented as follows:

x1= 4/3 + (1/3)x3 - (5/3)x4
x2= 2 + (1/3)x3 + (1/3)x4
x3= Free
x4= Free

How do I put the above solution into vector form as illustrated in the original question?

 

[Euge]

Hi ibwev,

If you set the free variables $x_3, x_4$ equal to zero, you find that $\begin{bmatrix}4/3 & 2 & 0 & 0\end{bmatrix}^T$ is a particular solution. So the general solution can be written$$x = \begin{bmatrix}4/3\\2\\0\\0\end{bmatrix} + x_3\begin{bmatrix}1/3\\1/3\\1\\0\end{bmatrix} + x_4\begin{bmatrix}-5/3\\1/3\\0\\1\end{bmatrix}.$$

 

[ibwev]

Thank you so much. I have been trying to figure this out for 2 days. I really appreciate the help.

 

[ibwev]

View attachment 4016

Please see question and correction on image.

 

[Euge]

The $1$'s come from the trivial equations $x_3 = x_3$ and $x_4 = x_4$.

 

[Prove It]

The $1$'s come from the trivial equations $x_3 = x_3$ and $x_4 = x_4$.

Most people use a parameter for the free variables, such as $ t = x_4 $ and $ s = x_3 $. It is much easier to see the vector form of the line of solution (or in this case, hyper-line of solution).

 

[Euge]

I want to make it clear that in practice I use different letters in place of the free variables to express the general solution parametrically.