- #1
Gackhammer
- 13
- 0
Hey
So, I was wondering how to convert from one coordinate axes to another... in particular, where the new axes are y = x and y = -x, as seen by the picture below
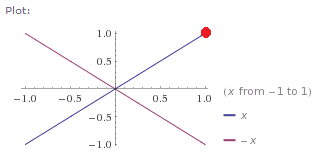
I want it so that the Red dot in the new coordinate system will be ([itex]\sqrt2[/itex],[itex]0[/itex]). Is there an easy way to do this? (My lookings on the internet have not come up with anything good yet)
EDIT: Ok, I just found the equations to rotate, but I was wondering how I can write functions in this rotated coordinate system (Im trying to relate this to my recurrences work/fixed point stuff). I am trying to rotate the coordinate system then find the zeros in the rotated coordinate system to find the fixed points of the function
So, I was wondering how to convert from one coordinate axes to another... in particular, where the new axes are y = x and y = -x, as seen by the picture below
I want it so that the Red dot in the new coordinate system will be ([itex]\sqrt2[/itex],[itex]0[/itex]). Is there an easy way to do this? (My lookings on the internet have not come up with anything good yet)
EDIT: Ok, I just found the equations to rotate, but I was wondering how I can write functions in this rotated coordinate system (Im trying to relate this to my recurrences work/fixed point stuff). I am trying to rotate the coordinate system then find the zeros in the rotated coordinate system to find the fixed points of the function
Last edited: