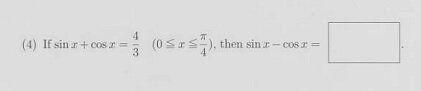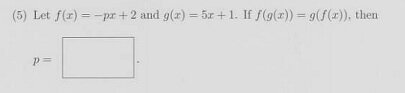Discussion Overview
The discussion revolves around the correctness of resolutions for two mathematical problems involving trigonometric identities and algebraic manipulations. Participants explore various methods to solve the equations, including squaring terms, applying Pythagorean identities, and proposing alternative approaches.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant presents an equation involving sine and cosine, suggesting a squaring method to derive further identities.
- Another participant proposes an algebraic approach to find the value of a variable, questioning the correctness of previous algebraic steps.
- Some participants reiterate the squaring method and apply Pythagorean identities, leading to different interpretations of the results.
- A later reply introduces a linear combination approach to express the sine and cosine terms, suggesting a transformation to simplify the problem.
- Another participant points out a potential error in algebraic manipulation, emphasizing the need to check calculations carefully.
- Some participants explore the implications of the results, discussing the conditions under which certain roots should be taken based on the range of x.
- One participant provides a more general solution that avoids trigonometric equations, proposing a substitution method to derive sine values directly.
Areas of Agreement / Disagreement
Participants express differing views on the correctness of the algebraic manipulations and the application of identities. There is no consensus on the final resolutions, as multiple competing methods and interpretations are presented throughout the discussion.
Contextual Notes
Some participants note limitations in their approaches, such as assumptions about the ranges of sine and cosine, and the dependency on specific algebraic steps that may not have been fully resolved.
Who May Find This Useful
Readers interested in trigonometric identities, algebraic manipulation, and problem-solving techniques in mathematics may find this discussion beneficial.