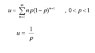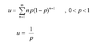Is the Proof of Geometric Progression in Probability Common Sense?
Click For Summary
The discussion centers on the proof of the expected value in a geometric distribution, specifically the formula $$E[X] = \frac{1}{p}$$, where \(p\) is the probability of success. Participants emphasize the importance of the Binomial Theorem and the memoryless property of geometric distributions in deriving this result. The conversation highlights the necessity of understanding convergence issues and suggests using derivatives to simplify the summation involved in the proof. Ultimately, the participants agree that while the proof may not be presented in textbooks, it is mathematically sound and intuitive.
PREREQUISITES- Understanding of geometric distributions and their properties
- Familiarity with the Binomial Theorem
- Knowledge of expected value calculations in probability
- Basic concepts of convergence in infinite series
- Study the derivation of expected values in geometric distributions
- Learn about the memoryless property of geometric distributions
- Explore the application of the Binomial Theorem in probability
- Investigate convergence issues in infinite series and their implications
Statisticians, mathematicians, and students studying probability theory, particularly those interested in geometric distributions and their applications in real-world scenarios.
Similar threads
- · Replies 4 ·
- · Replies 1 ·
- · Replies 5 ·
- · Replies 13 ·
- · Replies 3 ·
- · Replies 2 ·
- · Replies 3 ·
- · Replies 5 ·
- · Replies 17 ·
- · Replies 4 ·