Covering Maps and Liftings - Munkres Theorem 54.4

[Math Amateur]

I am reading Munkres book Topology.

Currently, I am studying Section 54: The Fundamental Group of the Circle and need help with a minor point in the proof of Theorem 54.4

Theorem 54.4 and its proof reads as follows:

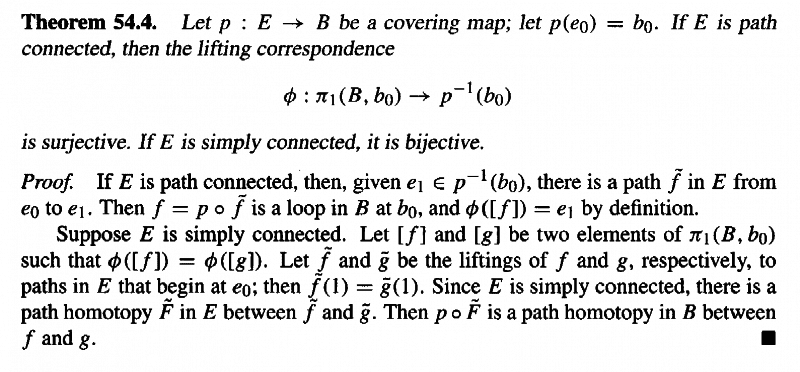
In the proof we read:"If $E$ is path connected, then, given $e_1 \in p^{-1}(b_0)$, ... ... "... ... BUT ... ... how do we know there exists an $e_1$ different from $e_0$ in $p^{-1}(b_0)$ ... maybe $e_0$ is the only element in $p^{-1}(b_0)$?

What, indeed, do we know about the nature of $p^{-1}(b_0)$?

Hope someone can help ...

Peter

 

[mathwonk]

he is trying to prove surjectivity, i.e. that every element of p^(-1)(b0) occurs as a lift. so he starts by taking any point in p^(-1)(b0) and produces a lift that gives it. I.e. his statement is: "IF e1 is a point of p^(-01)(b0), then e1 occurs as a lift." He is not assuming any such e1 exists that is different from e0. Indeed if none did exist, surjectivity would be trivial, since the lift of the identity element of the fundamental group would give the unique point e0. Note his proof works also when e1 = e0.

 

[Math Amateur]

he is trying to prove surjectivity, i.e. that every element of p^(-1)(b0) occurs as a lift. so he starts by taking any point in p^(-1)(b0) and produces a lift that gives it. I.e. his statement is: "IF e1 is a point of p^(-01)(b0), then e1 occurs as a lift." He is not assuming any such e1 exists that is different from e0. Indeed if none did exist, surjectivity would be trivial, since the lift of the identity element of the fundamental group would give the unique point e0. Note his proof works also when e1 = e0.

Thanks for the reply mathwonk ... Most helpful

Peter