Crystals- filling a tetrahedral site.

[Beer-monster]

Homework Statement

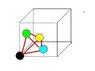
I'd like to work out what the largest sphere I could fit in the tetrahedral interstitial site of a cubic unit cell. Preferably I believe I need an expression in terms of the lattice constant a.

Homework Equations

The Attempt at a Solution

The tetrahedral site is at the centre of a 'minicube' defined by dividing each of the major lattice planes of the unit cell in half (resulting in 8 such 'minicubes' with edge length a/2).

Using this fact I thought I could work out the free space available by taking the total volume of the tetrahedron and subtracting the volume of the sphere fractions contained within the tetrahedron. Then working out the size of a sphere corresponding to the that free space.

However, this is proving rather messy and complicated (mainly due to working out what fraction of the spheres are contained in the tetrahedron). Also, I think I'm looking for a general solution and my method would differ if it was fcc or bcc cubes.

Could anyone point me in a better direction?

Thanks

 

[ehild]

Start arranging spheres according to the close-packed structure so as the spheres touch each other, and find the empty space among them. See for example http://departments.kings.edu/chemlab/animation/clospack.html

ehild

 

[Beer-monster]

I'm not sure I follow.

Even if I could find the volume of the empty space, all of it would not be filled by a sphere (there would still be some empty space) and I'm not sure I can work out the fraction of space occupied to convert to radius of a sphere.

 

[ehild]

Do not calculate with volumes.

ehild

 

[Beer-monster]

After giving it some thought, I've figure that the maximum diameter of the interstitial sphere should equal the difference between the body diagonal of the cube and the space take up by the close-packed spheres (i.e. twice the sphere radius).

Does this sound like its on the right track?

 

[ehild]

It is OK for a simple cubic cell, but it is not the so called close-packed structure. And it is not a tetrahedral site.

ehild

 

[Beer-monster]

If I divide the cube into 8 minicubes. the corners of each minicube being one corner and three face atoms from the original lattice. I can find the body diagonal of such a minicube and then deduct two atomic radii, leaving the diameter of the empty space?

I've tried the above but seem to be having some difficulty solving the sum.

$$\frac{\sqrt{3}}{\sqrt{2}}a-\frac{a}{\sqrt{2}}$$

But I think its the late hour and me being dense.

 

[ehild]

The nearest atoms are at the ends of the face diagonals of the mini-cubes, at the corners of a tetrahedron.

ehild

 

[Beer-monster]

I see. I must have been drawing my tetragons very badly.

Considering your diagram and this one
http://www.tf.uni-kiel.de/matwis/amat/def_en/kap_1/illustr/t1_3_4.html

I can see that each vertex is a face diagonal, which touch for a close-packed or fcc structure. So the only dimension I can consider that contains the 'gap' is the height of the tetrahedron. However, I can deduct the radius of the top atom but the other end is more difficult since I'm trying to deduct the 'height' of the hollow site.

 

[ehild]

The centre of the circumsphere of the tetrahedron is also the centre of the sphere inscribed in the gap between the atoms. Find the radius of the inscribed sphere, and subtract the radius of an atom which is half the edge length of the tetrahedron.

ehild

 

[Beer-monster]

Okay, based on some drawing. I realized that the radius of the circumsphere is half the body diagonal of the minicube and the radius of the atom is half the face diagonal. That leaves

$$\frac{\sqrt{3}a}{4} - \frac{a}{2\sqrt{2}}$$

Which I can't work out how to simplify.

 

[ehild]

You can make it a little bit nicer by using 4 as common denominator.

ehild

 

[Beer-monster]

So

$$\frac{\sqrt{3}a}{4} - \frac{\sqrt{2}a}{4}$$

 

[ehild]

What about factoring a/4 out ? And evaluating √3-√2?

ehild

 

[Beer-monster]

That dos make things neater but I' m finished then correct, because I can,t add/subtract unlike radicals.

 

[ehild]

You can let it as it is, or give the approximate value: 0.07946 a.

ehild