Discussion Overview
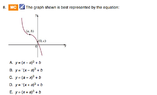
The discussion revolves around understanding horizontal transformations of cubic functions, specifically how to interpret graphs represented by equations of the form f(x+a) and f(x-a). Participants explore the implications of these transformations on the graph's position and shape.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
Main Points Raised
- Some participants express confusion regarding the interpretation of horizontal transformations and how they affect the graph's position along the x-axis.
- One participant suggests a rule of thumb for determining the direction of horizontal translations, stating that f(x+a) moves the graph a units to the left and f(x-a) moves it a units to the right.
- Another participant proposes that the equation f(x)=-(x-a)^3 +b is a potential representation of the graph, but questions arise about its validity.
- Concerns are raised about the implications of comparing different cubic functions, particularly regarding the direction of the graph and the effects of transformations.
- One participant notes that when x=a, y=b, which leads to the elimination of certain options based on the behavior of the cubic function.
- A question is posed about the implications of using (-a,b) instead of (a,b) in the context of the transformations discussed.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the correct interpretation of the transformations or the validity of the proposed equations. Multiple competing views and interpretations remain present throughout the discussion.
Contextual Notes
Participants rely on specific assumptions about the behavior of cubic functions and their transformations, but these assumptions are not universally agreed upon. The discussion also highlights the complexity of interpreting graphical representations of mathematical functions.