Discussion Overview
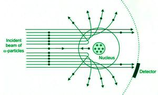
The discussion revolves around the De Broglie–Bohm theory, particularly focusing on the nature of particle trajectories in the context of scattering from a point charge, such as in Rutherford scattering. Participants explore the implications of non-crossing trajectories and how they relate to classical and quantum mechanics, as well as the observable nature of these trajectories.
Discussion Character
- Debate/contested
- Technical explanation
- Conceptual clarification
- Mathematical reasoning
Main Points Raised
- Some participants question whether the trajectories in the De Broglie–Bohm theory can cross, particularly in the context of Rutherford scattering.
- There is a suggestion that the term "trajectory" may have different meanings in classical versus quantum contexts, leading to potential misinterpretations when comparing images of trajectories.
- One participant asserts that classical and quantum explanations of scattering are fundamentally different, despite coinciding differential cross sections.
- Another example is provided where Bohmian trajectories differ significantly from classical trajectories, specifically in the Mach-Zehnder interferometer scenario.
- Concerns are raised about the observability of Bohmian trajectories, with some arguing that they are not observable, while others suggest weak measurements could provide insights.
- Participants discuss the implications of measuring trajectories on the cross section in Coulomb-scattering events, noting that strong measurements would distort results.
- There is speculation about whether the De Broglie–Bohm trajectories actually cross, with references to simpler problems like scattering on a potential barrier to illustrate the complexity of the topic.
- Some participants argue that in stationary wave functions, trajectories do not cross at the same time, while others suggest that in non-stationary cases, crossings can occur at different times.
- Clarifications are made regarding the relationship between the phase of the wavefunction and the behavior of trajectories, particularly in the context of interference and scattering.
Areas of Agreement / Disagreement
Participants express differing views on whether Bohmian trajectories can cross, with some asserting they do not cross at the same time while others suggest crossings can occur under certain conditions. The discussion remains unresolved regarding the implications of these trajectories in scattering scenarios.
Contextual Notes
Limitations include the dependence on definitions of trajectories, the nature of wavefunctions (stationary vs. non-stationary), and the assumptions made in comparing classical and quantum models. The discussion also highlights the complexity of visualizing and interpreting Bohmian trajectories in various contexts.

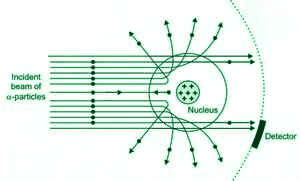 Thanks.
Thanks.