physics604
- 92
- 2
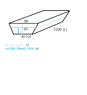
1. A water trough is 10 m long and a cross-section has the shape of an isosceles trapezoid that is 30 cm wide at the bottom, 80 cm wide at the top, and has height 50 cm. If the trough is being filled with water at the rate of 0.2 m^3/min, how fast is the water level rising when the water is 30 cm deep?
$$V=\frac{(a+b)h}{2}×L$$
Given (I converted all to cm):
$$a=30$$ $$\frac{da}{dt}=0$$ $$base=80$$ $$height=50$$ $$\frac{dV}{dt}=0.2$$ $$h=30$$ $$L=10$$ $$\frac{dL}{dt}=0$$
I need to find $$\frac{dh}{dt}$$
After I find the derivative of V using natural log.
$$lnV=\frac{1}{2}ln(a+b)hL$$
$$lnV=\frac{1}{2}ln(a+b)+lnh+lnL$$
$$\frac{dV}{dt}=\frac{1}{2}(\frac{db/dt}{a+b}+\frac{dh/dt}{h})×V$$
I don't know how I'm supposed to find $$\frac{db}{dt}$$ i get b=60.
Any help is much appreciated.
Homework Equations
$$V=\frac{(a+b)h}{2}×L$$
The Attempt at a Solution
Given (I converted all to cm):
$$a=30$$ $$\frac{da}{dt}=0$$ $$base=80$$ $$height=50$$ $$\frac{dV}{dt}=0.2$$ $$h=30$$ $$L=10$$ $$\frac{dL}{dt}=0$$
I need to find $$\frac{dh}{dt}$$
After I find the derivative of V using natural log.
$$lnV=\frac{1}{2}ln(a+b)hL$$
$$lnV=\frac{1}{2}ln(a+b)+lnh+lnL$$
$$\frac{dV}{dt}=\frac{1}{2}(\frac{db/dt}{a+b}+\frac{dh/dt}{h})×V$$
I don't know how I'm supposed to find $$\frac{db}{dt}$$ i get b=60.
Any help is much appreciated.
Attachments
Last edited: