kahwawashay1
- 95
- 0
I'm not understanding how the equation of the electric field due to an electric dipole is derived. This is how my book derives it:
Say you have electric dipole composed of charges +q and -q a distance d apart, with the negative charge at the origin of the z-axis. Then, at any point z, the E field is:
\frac{kq}{(z-\frac{1}{2}d)^{2}} - \frac{kq}{(z+\frac{1}{2}d)^{2}}
Below is the exact picture of the situation from my book:
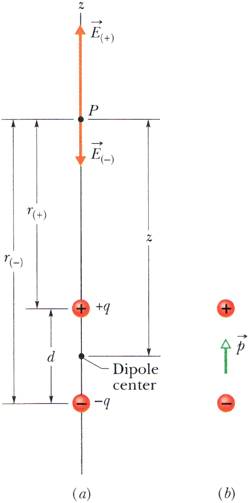
But shouldn't the equation be:
\frac{kq}{(z-d)^{2}} - \frac{kq}{z^{2}}
??
In my book's equation, it looks like they're just treating the two charges as if they're at the same point (the midpoint, corresponding to (1/2)d)...I know that for large z, this wouldn't matter much, but still, what if you want small z...
Say you have electric dipole composed of charges +q and -q a distance d apart, with the negative charge at the origin of the z-axis. Then, at any point z, the E field is:
\frac{kq}{(z-\frac{1}{2}d)^{2}} - \frac{kq}{(z+\frac{1}{2}d)^{2}}
Below is the exact picture of the situation from my book:
But shouldn't the equation be:
\frac{kq}{(z-d)^{2}} - \frac{kq}{z^{2}}
??
In my book's equation, it looks like they're just treating the two charges as if they're at the same point (the midpoint, corresponding to (1/2)d)...I know that for large z, this wouldn't matter much, but still, what if you want small z...
Last edited: