Deriving Actuator Force Equations for Scissor Lift Design

[Autosug]

Hi.

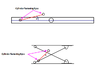
I am currently working on a scissor lift design. I'm having some trouble deriving the equations for the actuator force for some reason. Think I'm getting blind on this ATM or something :P. Anyways if someone could help a bit id appreciate it. [I have derived equations I'm just not sure I did it all the right way]
I have all information but the reactions and force in the actuator. Only seeking some standard derivation to se if I did correct or not :) [all other information is available) And actuator is placed between scissor arms.
The scissor lift will start from bottom and up. So the alpha angle is small.

Se picture

 

[Simon Bridge]

I have derived equations I'm just not sure I did it all the right way.

Show us please.
Otherwise you are basically using us as free engineering consultants.
Show us and we can help you see where you are having trouble and everyone benefits.

 

[Autosug]

Just to be clear. I am not trying to get any free stuff[close to getting my diploma...) :)
But I understand you and its fine. I have added the pictures in the PDF hope it helps.
Note: X1 is known and alpha to.

Edit: And as far as i se i have to many unknown compared to equations. So I am thinking i do something not right even more (maybe the way I look at the system...) :)
regards

 

[Autosug]

No one has any ideas?

 

[Simon Bridge]

You have yet to explain what you've done - all I see are a bunch of anonymous lines and equations.
Please annotate your work so someone completely unfamiliar with what you've done can follow your reasoning.

I'm guessing the red line on the diagram is some sort of actuator - but no idea how it is supposed to act and, anyway, one end appears to be unsupported. It appears the angle of the red line is supposed to change in operation ... ?

So no ... considering the number of possible ways a scissor lift could work: not a clue.

 

[Autosug]

Red Line is the cylinder.
As shown on the attachment in my first post there are two cylinder fastening eyes where the cylinder is fastened. The scissor lift starts from collapsed state as I have tried to show in my first post attachment. When it raises, the left side of the lift moves towards the right because of the rollers on the scissor lift. Because the cylinder is attached to the scissor arms through the fastening eyes on the left side of the scissor, the cylinder will move towards the right with the scissor when the scissor is raised.
My problem is: Do I look at this system the right way concerning the way I have put forces on the system. Or is there something I miss. Because as stated in my second post I think I have to many unknowns atm. so It is indeterminate..
Hope this helps :)

 

[Simon Bridge]

OK, so the red line is a piston thing using hydraulics or pneumatics?
When the scissor arm is horizontal, the piston makes an angle alpha to the horizontal ... but it appears to rotate with the scissor arm it is attached to so the angle to the scissor arm is always the same?

What is the other end of the piston attached to?
In both diagrams it is just floating there.

Under what conditions do you want to calculate the force - force to do what?
Perhaps you want to lift the platform at a constant speed, hold it at a constant height, or accelerate it?

 

[Autosug]

The system will work with hydraulics. The attachment close to the center of the scissor is attached through brackets that are welded on a middle beam between the scissor arms. This bracket is in front and above the center of the scissor arms so lift can happen. The other cylinder end is also attached via brackets that are also welded on a beam between the scissors at the end. This will ensure the cylinder stays in place. (I see now that it was a mistake to put alpha on the second drawing of attachment one. This angle will change a bit if i am correct).
Anyways the thing i actually seek is the force acting in the cylinder at the very moment the scissor starts to lift. This is so I can determine a proper cylinder size for my system. And it will ofc. be with maximum load on the scissor system. And that's where the trouble starts :)
(I have been working on the whole thing for some months now sot hat might be why I just have answered shortly. I have a lot in my head and stuff seems obvious to me. I know It is not to all :) But I hope this helps else let me know and Ill see if i can come up with something different.)

 

[Simon Bridge]

Oh OK - so the "unattached" end of the cylinder should actually be treated as fixed in the reference frame of the ground?

I doubt that the arrangement will actually lie flat like the diagram when the platform is completely lowered.
Apart from that - you want to position the forces of the weights of everything the cylinder has to lift as well as resolve the forces into those that act along the scissor arms and those that act perpendicular to the arms.

I think your should be able to use the instantaneous torques for this.

Have you looked at how other problems have been done?
http://www.engineersedge.com/mechanics_machines/scissor-lift.htm
https://www.physicsforums.com/showthread.php?t=449843

 

[Autosug]

Well i have already the basic design ready in CREO for the scissor. So I wanted to know the force that would act in the cylinder. I was hoping by simplifying the system it could be viewed as a static simple system, because the scissor system was laying flat down when collapsed and then just view it the way I showed in the pdf file. I also have a factor of safety of 2 which also should make up for friction in joints and so on. Now I am not so sure I can do it that easy.
Anyways thank you for you reply I will look into it again and see what I can come up with:)

Regards

 

[Simon Bridge]

Cool ... for the situation you are trying for, the cylinder only supports one side ... I guess you could do a back-of-envelope by treating the entire thing as a loaded beam.