How to translate force into upward hinging motion between two panels?

[mmcnaught831]

TL;DR Summary

How to create a hinged joint between two panels where the hinging motion is actuated simply by pushing the panels together as they lie flat?

Pictured below are two hinged panels that can rotate upward to form an upside-down V. In position 1, the panels are lying flat. In position 2, the panels have folded together and the joined edge is raised up.
Normally, in order to actuate this hinging motion, one would need to manually lift the joined edges upward, initiating the hinge motion, and then push/slide the panels together to continue the motion.

I would like to create a mechanism in which the hinging motion is actuated merely by pushing the two panels towards each other as they lie flat (in Position 1).

In the image below, I've drawn a simple diagram of how such a motion is possible using shapes of a different geometry. Having a mitered corner where two blocks butt up against each other allows for this "hinging" motion to be actuated merely by pushing the blocks together, so long as the elevation of the applied force is lower than the hinge point.

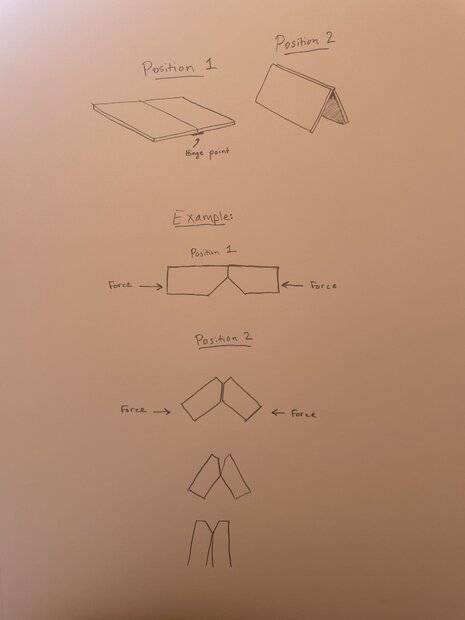
I am wondering how the physics of this movement could be applied to the two panel design.
The issue that I am encountering is that the elevation of the applied force is equal to the elevation of the hinge point, which basically seems to prevent the hinging motion from occurring. Even with mitered edges along the panels, pushing Panel 1 toward Panel 2 results in no motion, just wasted force.

Is there a way to translate this force into the hinge motion? Is there some physical law that is preventing this from happening? What would need to be the case in order for the hinging motion to be actuated simply by pushing one panel toward the other?If anybody has a suggestion as to how this mechanism would be possible, I would be most grateful.

***One design constraint that I would like to hang on to is for there to be zero movement in the panels except for the hinge mechanism. I.e., I would not like for the panels to be separated from each other in Position 1. Position 1, ideally, would be a continuous flat surface.

Thank you!

 

[Dr.D]

If the force is applied below the hinge pin centerline, this will give rise to a moment that will cause the hinge to rise. That should be all you need.

 

[jrmichler]

Yes, it can be done. Depending on the size and weight of the panels, the force could be quite high. You will need to put the hinge pin as high as possible, and apply the force as low as possible. See Figure 1 in the diagram below:

Calculate the force as follows (Figure 2 above):
1) The weight of one panel is mg.
2) The distance from the center of gravity of one panel to the edge where the force is applied is D.
3) The vertical distance from the hinge pin to the point of force application is d.
4) The force to start the panels folding is mg X D / d.

Example calculation for panels 10" wide, weighing 5 lbs, and d is 1 inch:
Force needed = 5 lbs X 5" / 1" = 25 lbs. Since the other panel is a mirror image, the force on the other side is equal to the force on the first side. You can try realistic dimensions to find the force in your application.

Figure 3 shows a way to hide the hinge. I suggest using a piano hinge for this. Here is a good source with a large variety of piano hinges: https://www.mcmaster.com/piano-hinges/piano-hinges-with-holes/

 

[Lnewqban]

Just an idea:
https://www.aliexpress.com/i/1005001562288997.html

 

[mmcnaught831]

Just an idea:
https://www.aliexpress.com/i/1005001562288997.html

Thank you very much. I didn't know about these, I will definitely look into them and see if they may have applications in my project.