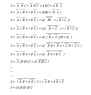Deriving full adder sum and carry outputs using boolean algebra

[dannyres]

Homework Statement

Hi, I am trying to write the sum and output of a full adder in terms of XOR logical functions using boolean logic and Karnaugh maps. I've got the expressions from the Karnaugh maps fine but I can't seem to rearrange them into the expected form shown at the end of my working.

Homework Equations

Explained above.

The Attempt at a Solution

It's going to be difficult writing my working here but hopfully it is clear:

My equation obtained from the Karnaugh map using a minimized SOP:
Sum = NOT(A).NOT(B).C + NOT(A).B.NOT(C) + A.B.C + A.NOT(B).NOT(C)
Sum = NOT(A).(NOT(B).C + B.NOT(C)) + A.(B.C + NOT(B).NOT(C))
Sum = NOT(A).(B XOR C) + A.(B.C + NOT(B).NOT(C))

..
...
...

Sum = NOT(NOT(A).B + A.NOT(B)).C + (NOT(A).B + A.NOT(B)).NOT(C)
Sum = (A XOR B) XOR C

This is where I'm trying to get. I've tried going both backwards and forwards but I just don't know where to go in-between. Any suggests to get me past the 3rd step I'm at?

Thank you,
Dan

 

[dannyres]

I've made some significant progress but I've become stuck again.. here is what I've got:

 

[berkeman]

Ouch. Welcome to the PF. This is a 3-bit full-adder? Could you post the truth table, including the carry bit? But then how do K-maps help in an XOR implementation of the truth table? I don't think I've ever had to morph into XOR logic (must be an academic thing?) -- what are the techniques for going from traditional minterm implementations (K-maps) to XOR logic?