Discussion Overview
The discussion revolves around the derivation and interpretation of the gravitational constant G, exploring its relationship with other constants such as the permittivity of free space (ε) and the Coulomb force constant (k). Participants examine the geometric implications of the equations involved and the conceptual underpinnings of gravitational and electrostatic forces.
Discussion Character
- Exploratory
- Debate/contested
- Technical explanation
Main Points Raised
- One participant seeks to express G in terms of π, r, ε, and k, suggesting a geometric interpretation of the r² term in the gravitational force equation.
- Another participant asserts that G is an independent constant and cannot be derived from other constants, emphasizing that it must be measured rather than calculated.
- A different viewpoint suggests that while G can be expressed algebraically in relation to ε, the resulting constant lacks physical meaning.
- Some participants note the similarity between the gravitational and Coulomb forces due to their spherical symmetry, hinting at potential deeper significance in physics.
- One participant introduces the concept of gravitational permittivity and permeability in the context of linearized General Relativity, suggesting analogies to electromagnetic constants.
- Another participant questions the relationship between G and r in Newton's law, seeking clarification on the implications of the constants involved.
Areas of Agreement / Disagreement
Participants express differing views on the relationship between G and other constants, with some asserting that G is independent while others propose potential connections. The discussion remains unresolved, with no consensus on how G can be derived or related to other constants.
Contextual Notes
Participants highlight the historical and conceptual differences between gravitational and electromagnetic forces, noting that gravity does not involve dipoles and behaves consistently inside and outside of matter. The discussion also touches on the limitations of current understanding regarding the physical meaning of constants related to G.
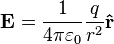 Any help would be appreciated. Thanks.
Any help would be appreciated. Thanks.