Ngineer
- 62
- 1
Homework Statement
Starting with the second order polarization in the time domain:
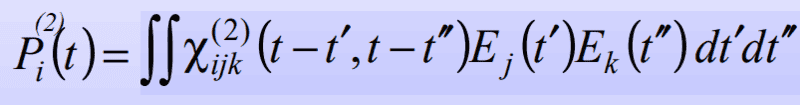 (1)
(1)
I am trying derive the frequency domain form:
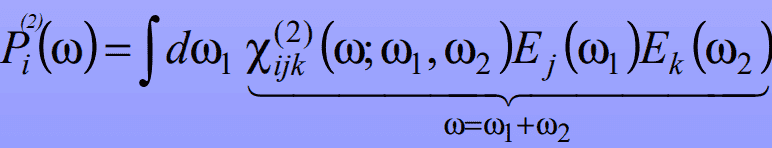 (2)
(2)
Multiple sources give essentially the same formula with the same integral, I have obtained the particular ones in here from those lecture notes.
My issue is finding the origin of the ∫dω1 integral. After a day of attempts I still can't figure out how it comes into play.
The attempt at a solution
Attempt 1
I started by identifying the time-domain formula (equation 1) as a double convolution:
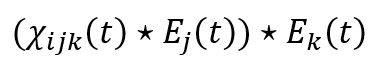
Which would map nicely to
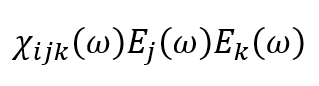
But I did not get far as to deriving equation 2 from here.
Attempt 2
Another approach I have attempted is that recognizing the the desired frequency-domain form (equation 2) is very close to convolution with respect to ω=ω1+ω2:
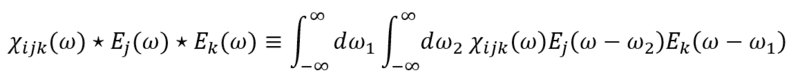
However,
- Why would a convolution in the time domain map to a convolution in the frequency domain?
- The original formula (equation 2) does not have an integral with respect to ∫dω2.
Any help is incredibly appreciated.
Thank you!
Starting with the second order polarization in the time domain:
I am trying derive the frequency domain form:
Multiple sources give essentially the same formula with the same integral, I have obtained the particular ones in here from those lecture notes.
My issue is finding the origin of the ∫dω1 integral. After a day of attempts I still can't figure out how it comes into play.
The attempt at a solution
Attempt 1
I started by identifying the time-domain formula (equation 1) as a double convolution:
Which would map nicely to
But I did not get far as to deriving equation 2 from here.
Attempt 2
Another approach I have attempted is that recognizing the the desired frequency-domain form (equation 2) is very close to convolution with respect to ω=ω1+ω2:
However,
- Why would a convolution in the time domain map to a convolution in the frequency domain?
- The original formula (equation 2) does not have an integral with respect to ∫dω2.
Any help is incredibly appreciated.
Thank you!
Attachments
-
 upload_2018-12-6_5-5-58.png7.7 KB · Views: 686
upload_2018-12-6_5-5-58.png7.7 KB · Views: 686 -
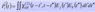 upload_2018-12-6_5-13-6.png8.5 KB · Views: 687
upload_2018-12-6_5-13-6.png8.5 KB · Views: 687 -
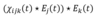 upload_2018-12-6_5-21-43.png1.8 KB · Views: 465
upload_2018-12-6_5-21-43.png1.8 KB · Views: 465 -
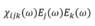 upload_2018-12-6_5-27-26.png1.5 KB · Views: 464
upload_2018-12-6_5-27-26.png1.5 KB · Views: 464 -
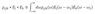 upload_2018-12-6_5-38-41.png5.3 KB · Views: 436
upload_2018-12-6_5-38-41.png5.3 KB · Views: 436 -
 upload_2018-12-6_5-46-59.png5.2 KB · Views: 466
upload_2018-12-6_5-46-59.png5.2 KB · Views: 466 -
 upload_2018-12-6_5-47-11.png5.2 KB · Views: 441
upload_2018-12-6_5-47-11.png5.2 KB · Views: 441 -
 upload_2018-12-6_5-52-57.png4.8 KB · Views: 478
upload_2018-12-6_5-52-57.png4.8 KB · Views: 478