Describing recursive formulae in words

[mse14]

Homework Statement

Recursive formulae and total probability

Relevant Equations

Consider two jars, each initially containing an equal number of balls. We perform four successive ball exchanges. In each exchange, we pick simultaneously and at random a ball from each jar and move it to the other jar. Let $p_{i,n−i}(k)$ denote the probability that after $k$ exchanges, a jar will contain $i$ balls that started in that jar and $n−i$ balls that started in the other jar. Suppose we want to find $p_{n, 0}(4).$ We argue recursively, using the total probability theorem. We have

$p_{n, 0}(4) = \frac 1n \cdot \frac 1n \cdot p_{n - 1, 1}(3),$

$p_{n - 1, 1}(3) = p_{n, 0}(2) + 2 \cdot \frac{n - 1}{n} \cdot \frac 1n \cdot p_{n - 1, 1}(2) + \frac 2n \cdot \frac 2n \cdot p_{n - 2, 2}(2),$

$p_{n, 0}(2) = \ldots$

$\ldots$

I am only interested in the verbal descriptions of $p_{n, 0}(4), \ p_{n - 1, 1}(3)$.

The right hand side of $p_{n, 0}(4)$ describes the probability of choosing one ball from one jar and the probability of choosing one ball from another jar and the probability of one of the jars containing $n-1$ original balls together with a ball from the other jar. Is that correct?

For $p_{n - 1, 1}(3)$ we need the total probability law.

In pictorial form, the total probability law looks like this below:

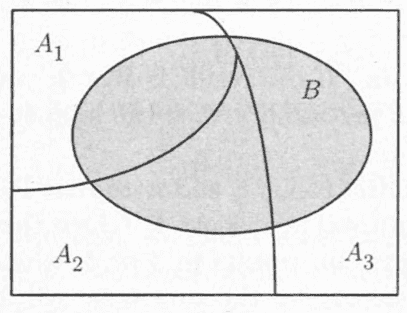
Using the notation from the pic above, we have $p(A_1) = p_{n, 0}(2), \ p(A_2) = p_{n-1, 1}(2), \ p(A_3) = p_{n-2, 2}(2)$. Assuming that's correct, what's $B$ here? Do we have two values for $B$, namely,$2 \cdot \frac {n-1}{n} \cdot \frac 1n$ and $\frac 2n \cdot \frac 2n$? Shouldn't $B$ have only one value? Also, shouldn't $p_{n, 0}(2)$ have a coeffcient, say $B$, according to the total probability law? Lastly, what probability does $2 \cdot \frac {n-1}{n} \cdot \frac 1n$ represent? I understand where the coefficient $2$ comes from, but not sure about the rest of the expression.

 

[haruspex]

I don't see why you need the total probability rule for this. It's just conditional probability.
To have it at (3,1) at one step either it was (4,0) at the prior step, or it was (2,2) and then we happened to pick exactly the right ball from each.
But to phrase it in the form you ask for, P(B) is what you are trying to find, $p_{3,1}(3)$. You would obtain this by summing $P(B|A_1)P(A_1)$ etc.

It is not quite clear how $p_{i,n−i}(k)$ is defined, but I would say that, for 2i<n, $p_{i,n−i}(k)$ and $p_{n−i, i}(k)$ represent distinct events.