Details regarding Legendre Polynomials

[MathewsMD]

I just had a few questions not directly addressed in my textbook, and they're a little odd so I thought I would ask, if you don't mind. :)

-Firstly, I was just wondering, why is it that Legendre polynomials are only evaluated on a domain of {-1. 1]? In realistic applications, is this a limiting factor? Is there a way to find solutions for a larger domain?

-Why exactly must n > -1?

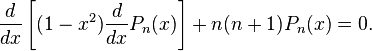
Is there a particular reason why it's only evaluated for these values of n? Is there an another approach for n < -1? Also, must n be a a non-negative integer or can n be any real number greater than -1?

-Is there a relatively short proof to prove $\int _{-1}^1 P_m P_n = \frac {2}{2n+1}; m = n$? All the ones I've seen are quite long and tedious, and are not as intuitive as the other case for $m \neq n$. I was just curious since I could not seem to find one.

Also, as a side question: what exactly happens to matrices that undergo elementary row operations? I know the column space is distorted and the row space is intact for elementary row operations, but what exact properties are now the same and different between a matrix A and a matrix A' derived from elementary row operations on A?

Also, why is it necessary Legendre polynomials pass through the point (1,1)? Why is this point unique?

Sorry for the questions! A few that were just lingering in my head that I wanted to address. Thank you!

 

[the_wolfman]

You're asking a lot of questions, and they're not all related. Legendre polynomials are pretty common, and a quick google search will provide more details than I can in a short response. Also I recommend looking into Sturm-Liouville theory. Many of your questions touch on ideas relevant to Sturm-Liouville, and they apply not only to Legendre polynomials, but also many many other commonly encountered special functions.

-Firstly, I was just wondering, why is it that Legendre polynomials are only evaluated on a domain of {-1. 1]? In realistic applications, is this a limiting factor? Is there a way to find solutions for a larger domain?

At $x=\pm1$ the nature of the differential equation changes drastically. If we expand out the equation we get
$\left(1-x^2\right)\frac{d^2}{dx^2} P_n -\left(2x\right)\frac{d}{dx}P_n +n\left(n+1\right) P_n =0$
we see that the coeficent infront of the second derivative is zero at $x=\pm1$. These points are singular points. The singular points bound the domain of validity of our solution. (Solutions normally can't cross singular points).

In practice the domain in not very limiting. Often when we encounter Legendre equations we have performed a transformation of variables such that $x=\cos{\theta}$. The the domain of {-1,1} is a natural choice.

Is there a particular reason why it's only evaluated for these values of n? Is there an another approach for n < -1? Also, must n be a a non-negative integer or can n be any real number greater than -1?

The Legendre functions are an extension of Legendre polynomials for any complex n. The functions are only polynomials for integer n. For negative n when can transform the equation using k = -n - 1. This transformation will yeild a Legendre equation for k, with $k\ge 0$. This implies that $P_{-n-1}\left(x\right) = P_n \left(x\right)$.

 

[Stephen Tashi]

are only evaluated on a domain of {-1. 1]? In realistic applications, is this a limiting factor?

If you had real life problem where a quantity like distance d varied between 120 meters and 300 meters, you could define a linear transformation between the variable d and a variable x so that x varied between -1 and 1. It would amount to picking a new origin for the zero of distance and picking a new scale of distance instead of using meters. A theme in physics is that if an equation describes a physical law correctly in one system of units of measurements, it is still valid when you transfom it by changing the units. You could also take the approach of transforming Legendre polynomials in x to different polynomials in the variable d.

 

[pasmith]

If you had real life problem where a quantity like distance d varied between 120 meters and 300 meters, you could define a linear transformation between the variable d and a variable x so that x varied between -1 and 1. It would amount to picking a new origin for the zero of distance and picking a new scale of distance instead of using meters. A theme in physics is that if an equation describes a physical law correctly in one system of units of measurements, it is still valid when you transfom it by changing the units. You could also take the approach of transforming Legendre polynomials in x to different polynomials in the variable d.

In addition, Legendre polynomials frequently arise as $P_n(\cos\theta)$ where $\theta \in [0,\pi]$ is a spherical polar coordinate, so the argument of $P_n$ is naturally in [-1,1].

 

[the_wolfman]

If you had real life problem where a quantity like distance d varied between 120 meters and 300 meters, you could define a linear transformation between the variable d and a variable x so that x varied between -1 and 1

I'm not sure that this is true for the Legendre equation? The domain of validity of the Legendre polynomials is limited by the singularities at $\pm 1$. If you linearly scale $x$ the location of these singularity will scale similarly. Thus the domain of validity scales too!

Another way to think about this is to consider the leading coefficient $\left(1-x^2\right)$. If you transform $ax = x'$ then this coefiicent in your new equation will be $\left(a^2-x'^2\right)$. Your new equation will only be a Legendre equation if $a=\pm 1$.

 

[Stephen Tashi]

Are you talking about scaling measurements of d to a new value x or are you talking about introducing some scaling factor into the polynomial? If you scale measurements of d into a scale for x that varies between -1 and 1, you don't need to do anything to the polynomial because you are working with x in the polynomials.

 

[Dr Transport]

Outside of x between -1 and 1, the Legendre polynomials are functions of cosh(x), per my well worn copy of Lebedev, Special Functions & Their Applications.

 

[the_wolfman]

Ahh, I think we are talking about slightly different things and we should be careful.

1) I'm talking about solving the different equation:
$\left( 1 -x^2\right)\frac{d y^2}{d x^2}-2x\frac{d y}{d x}+ l\left(l+1\right)y=0$
on a domain $\left[ a, b \right]$. Here the domain is critical. Unique solutions exist as long the domain does not cross the singular points $\pm 1$.

For instance the domains $\left[ 2, \infty \right]$ and $\left[ -.9, .9 \right]$ have unique solutions, but these solutions won't necessarily be Legendre polynomials.

However the domains $\left[ 0, 2 \right]$ and $\left[ -2, 2 \right]$ are problematic. Here a linear change of variables won't fix the problems.

2) There is a second problem. If you have a signal over a domain $\left[ a, b \right]$ we can analysis this signal using Legendre polynomials by linearly transforming the domain to $\left[ -1, 1 \right]$.