Determine ## \beta ## as a function of ##\theta## linkage

[erobz]

I 've been trying find $\beta$ as a function of $\theta$ for this linkage. It's quite the trigonometric mess.

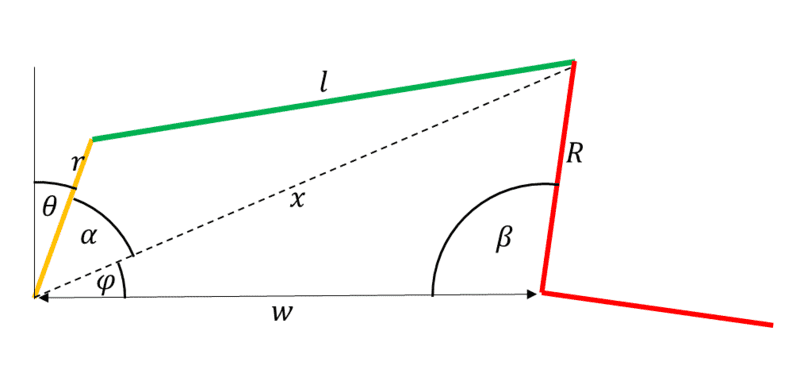
Start with the Law of Sines:

$$ \frac{\sin \beta}{x} = \frac{\sin \varphi}{R} \implies \boxed{ x = R \frac{\sin \beta}{\sin \varphi} \tag{1} }$$

Relating angles:

$$ \theta + \alpha + \varphi = \frac{\pi}{2} \implies \boxed{ \alpha = \frac{\pi}{2} -( \theta+\varphi) \tag{2} } $$

Applying Law of Cosines ( for each triangle):

$$ \boxed{ R^2 = w^2 + x^2 - 2 w x \cos \varphi \tag{3}}$$

$$ \boxed{ l^2 = r^2 + x^2 - 2 r x \cos \alpha \tag{4}}$$

Sub $(1) \to (3)$ to find $\sin \varphi$ in terms of $\sin \beta$:

$$ \left( \left( R^2-w^2\right)^2+ 4 w^2 R^2 \sin^2 \beta \right) \sin^4 \varphi - \left( 2R^2\left(R^2-w^2\right) + 4 w^2 R^2 \right) \sin^2 \beta \sin^2 \varphi + R^4 \sin^4 \beta = 0 \tag{5} $$

Eq $(5)$ can be solved for $\sin \varphi$ using the quadratic formula with the substitution $u = \sin^2 \varphi$:

$a = \left( \left( R^2-w^2\right)^2+ 4 w^2 R^2 \sin^2 \beta \right)$

$b = - \left( 2R^2\left(R^2-w^2\right) + 4 w^2 R^2 \right) \sin^2 \beta$

$c = R^4 \sin^4 \beta$

It follows that:

$$ \boxed{ \sin \varphi = \sqrt{ \frac{-b \pm \sqrt{b^2 - 4ac} }{2a} } \tag{6} } $$

Now, if we return to $(4)$ substituting $(1)$ and the identity $\cos \alpha = \sin ( \theta+ \varphi)$:

$$ l^2 = r^2 + \frac{R^2 \sin^2 \beta}{ \sin^2 \varphi}- 2 r \frac{R \sin \beta}{ \sin \varphi } \sin ( \theta + \varphi) $$

Then applying the sum-difference identity for $\sin( \theta + \varphi )$:

$$\boxed{ l^2 = r^2 + \frac{R^2 \sin^2 \beta}{ \sin^2 \varphi}- 2 r \frac{R \sin \beta}{ \sin \varphi } \left( \sin \theta \cos \varphi + \cos \theta \sin \varphi \right) \tag{7} }$$

From this point I can use a similar trick as in $5$ to get a solution for either $\sin \theta , \cos \theta$ in terms of $\sin \beta$ and all the constants.

It's seeming to be a real mess. Is it really this complex of a function - Have I messed up?

 

[andrewkirk]

I think you may find it easier to solve if you draw the other diagonal of the quadrilateral instead of the one labelled x. That diagonal goes from the top of the yellow line r to the vertex of the angle $\beta$. Call its length y.
Then, since you know the angle between r and w is $\pi/2 - \theta$ you can use the cosine rule for triangle r-y-w to get the length y in terms of $r,w,\cos(\pi/2-\theta)$, ie $r,w,\sin\theta$.
Next, use the sine rule for the same triangle to get the angle $\gamma$ in the bottom-right corner of that triangle. That forms part of the angle $\beta$.
The other part of $\beta$ is the bottom-right angle of the triangle l-R-y. You now know all three sides of that triangle, so you can apply the cosine law to that bottom right angle to get an expression for it in terms of $l,R,y$.

I don't know for sure that it's any less messy than what you had but since it really only has three steps: cosine rule, sine rule, cosine rule, I think it's likely to.

 

[erobz]

I think you may find it easier to solve if you draw the other diagonal of the quadrilateral instead of the one labelled x. That diagonal goes from the top of the yellow line r to the vertex of the angle $\beta$. Call its length y.
Then, since you know the angle between r and w is $\pi/2 - \theta$ you can use the cosine rule for triangle r-y-w to get the length y in terms of $r,w,\cos(\pi/2-\theta)$, ie $r,w,\sin\theta$.
Next, use the sine rule for the same triangle to get the angle $\gamma$ in the bottom-right corner of that triangle. That forms part of the angle $\beta$.
The other part of $\beta$ is the bottom-right angle of the triangle l-R-y. You now know all three sides of that triangle, so you can apply the cosine law to that bottom right angle to get an expression for it in terms of $l,R,y$.

I don't know for sure that it's any less messy than what you had but since it really only has three steps: cosine rule, sine rule, cosine rule, I think it's likely to.

Yeah, it does appear to be the elegant route:

$$ \beta = \arcsin\left( \frac{ r \cos \theta }{ \sqrt{ r^2+w^2-2rw \sin \theta} } \right) + \arccos\left( \frac{ r^2 +w^2+R^2-l^2-2rw \sin \theta }{ \sqrt{ r^2+w^2-2rw \sin \theta} } \right) $$

Simple change of perspective, dramatic effects...SMH. Thanks for the tip!