Discussion Overview
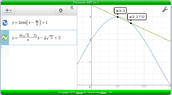
The discussion revolves around determining the average rate of change (AROC) of the function y = 2cos(x - $\pi$/3) + 1 over the interval from $\pi$/3 to $\pi$/2. Participants are exploring the calculations involved in finding the AROC and addressing discrepancies between their results and those presented in a textbook.
Discussion Character
Main Points Raised
- One participant attempts to calculate the AROC but reports an incorrect result of 1.4.
- Another participant provides a detailed calculation of the AROC, arriving at approximately 1.39811405542801, which matches the first participant's calculation.
- A third participant notes that the textbook provides a different value of -0.5157, suggesting that the textbook may be incorrect.
- A later reply identifies an error in the previous calculations, correcting the AROC to approximately -0.511745261674736 after graphing the function and the secant line.
Areas of Agreement / Disagreement
Participants do not reach consensus, as there are competing calculations and interpretations of the average rate of change, with some results differing significantly from others.
Contextual Notes
Participants' calculations depend on the accuracy of their evaluations of the cosine function and the interpretation of the interval endpoints. There are unresolved discrepancies between participant results and the textbook value.
