anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
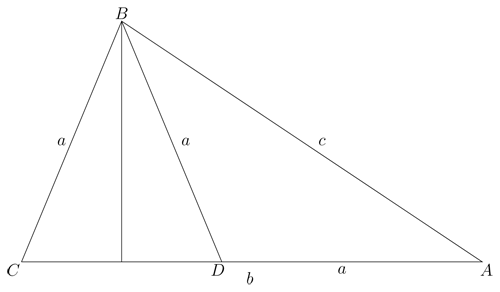
Let $$ABC$$ be a triangle such that $$\frac{BC}{AB-BC}=\frac{AB+BC}{AC}$$.
Determine the ratio $$\frac{\angle A}{\angle C}$$.
Determine the ratio $$\frac{\angle A}{\angle C}$$.