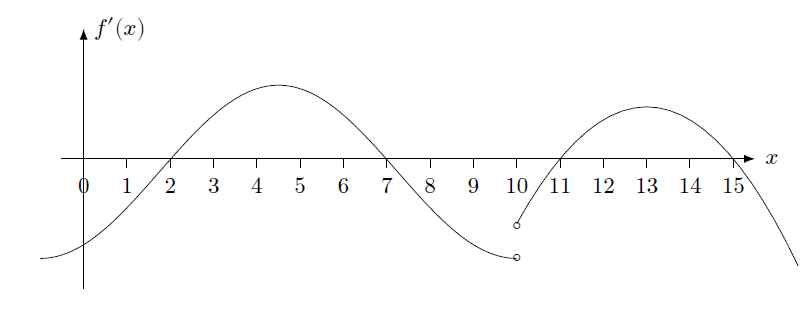Discussion Overview
The discussion revolves around determining critical points, intervals of increasing and decreasing functions, and identifying absolute maxima and minima on the graph of a function, specifically focusing on the derivative of that function. Participants explore these concepts through a provided graph and mathematical reasoning.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- Some participants inquire about finding critical points on the graph of the derivative of the function, questioning whether points at x=4.5 and x=13 are valid critical points.
- Participants discuss the intervals where the function is increasing, suggesting intervals such as [0,4.5] and (10,13].
- There is mention of intervals where the function is decreasing, with suggestions including [4.5,10) and [13, -∞).
- Some participants propose that the absolute maximum points could be at x=4.5 and x=13, while the absolute minimum might be at x=10.
- Questions are raised regarding the conditions under which relative maxima and minima occur, specifically focusing on where the derivative equals zero or is undefined.
- Participants reference a graph of the function to support their claims about increasing and decreasing behavior.
Areas of Agreement / Disagreement
There is no consensus on the validity of the critical points or the identification of maxima and minima, as participants express differing views on the conditions for these classifications. The discussion remains unresolved regarding the exact points and intervals.
Contextual Notes
Participants highlight the importance of understanding the behavior of the derivative in relation to critical points and the definitions of increasing and decreasing functions. There are unresolved questions about the continuity of the function and the implications of the graph provided.