vcsharp2003
- 913
- 179
- Homework Statement
- Four persons K, L, M, N are initially at the four corners of a square of side d. Each person now moves with a uniform speed v in such a way that K always moves directly towards L, L directly towards M, M directly towards N and N directly towards K. The four persons will meet after how much time?
- Relevant Equations
- v= d/t i.e. velocity = displacement/time
Relative velocity of A wrt B = velocity of A - velocity of B
The point of confusion is deciding the direction each persons sets out in i.e. velocity direction of each person. Knowing this will probably help in getting the solution.
At t=0, I can say that velocity of each person is as shown in diagram below.
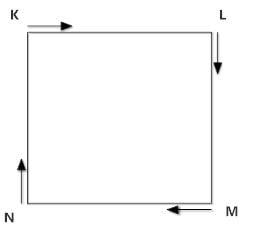
At t=0, I can say that velocity of each person is as shown in diagram below.
Last edited: