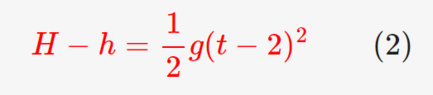Two balls, dropped with a delay of ##\Delta t##, meet after rebound

[erobz]

Hi @erobz, can you check your working that I put below which you did in post #18 above? I think you are off by a factor of 2. I put your workings on the right, with the mistakes in red ink.
View attachment 339076

Let me copy and paste what I am getting. I mark the final expression for $u$ in orange.

View attachment 339077

View attachment 339078What's more, I did not understand your reason for keeping the positive ($+$) sign for $u$. I copy and paste your reason to the right.

Indeed, $u = t-\sqrt{\frac{2H}{g}}$ and since $t>\sqrt{\frac{2H}{g}}\Rightarrow u>0$. But is that the reason to keep the $+$ sign?
See my reasoning below to the right on dark page.

View attachment 339081
What I am saying basically is that the second term is less than the first in the expression for $u$. So keeping the $-$ sign continues to keep $u>0$.

Many thanks.

Yes, you are correct on both accounts. I goofed on the algebra, and one of the solutions cannot be ruled out by negative time.

So if both solutions are positive for $u$, must we then take the smallest of the two as the desired solution? ( i.e. $u = \frac{1}{g}\sqrt{2gH} - \sqrt{\frac{2(H-h)}{g}}$ ) or do we just work with both solutions $\pm$ ( I'm leaning towards the former)?

 

[brotherbobby]

@erobz, you were right. I think I have solved it, though a question lingers. Since it has been sometime that I have posed the problem, let me state things from the beginning to refresh.

Attempt : Taking $g = 9.8\:\text{m/s}^2$, we have the equation of motion of the first ball as (see my post #1) shown on the right. Here $h$ is the height where the balls meet, $t$ is the time when they meet (from the start, when the first ball was dropped). The equation of motion of the second ball (see my post #1) is also shown on the right. The question is now to find the height of the cliff H (=?).

In $(1)$, let us put $\color{blue}{u = t-\sqrt{\frac{2H}{g}}}\qquad \color{brown}{(3)}$
This, after some algebra, we obtain $\small{u^2-\sqrt{\frac{8H}{g}}u+\frac{2h}{g}=0\Rightarrow u = \sqrt{\frac{2H}{g}}\pm\sqrt{\frac{2(H-h)}{g}}=\sqrt{\frac{2}{g}}(\sqrt H\pm \sqrt{H-h})}$
Substituting from $(3)$ for $u=t-\sqrt{\frac{2H}{g}}=\sqrt{\frac{2}{g}}(\sqrt H\pm \sqrt{H-h})\Rightarrow t = \sqrt{\frac{8H}{g}}\pm \sqrt{\frac{2(H-h)}{g}}$.
From equation $(2)$, we have $\sqrt{\frac{2(H-h)}{g}}=t-2\Rightarrow \color{blue}{t = \sqrt{\frac{8H}{g}}\pm (t-2)}\qquad \color{brown}{(4)}$

There are two possibilities to $(4)$ as evidenced by the $\pm$ sign.

$1. \;\mathbf{(-)\,\text{sign}}$ :

This yields from $(4)$, $2t-2 = \sqrt{\frac{8H}{g}}\Rightarrow t= \sqrt{\frac{2H}{g}}+1\Rightarrow t-\sqrt{\frac{2H}{g}}=1\quad(=u)$. Putting this value of $t$ in $(1)$, we have,
$\small{h = \sqrt{2gH}-\frac{1}{2}g\Rightarrow h+\frac{1}{2}g = \sqrt{2gH}\Rightarrow 55+5=\sqrt{20H}\quad\text{(putting values here)}\Rightarrow 60^2=20H\Rightarrow} \boxed{H = 180\,\text{m}}\quad\large{\color{green}{\checkmark}}$

This agrees with the answer.

$2. \;\mathbf{(+)\,\text{sign}}$ :

This yields from $(4)$, $t=\sqrt{\frac{8H}{g}}+t-2\Rightarrow \sqrt{\frac{8H}{g}} = 2\Rightarrow H = \frac{4g}{8}= 5\,\text{m}\quad\huge{\color{red}{\times}}$.

Of course this answer is incorrect, as the problem states that the ball collide at $h = 55\,\text{m}$. But it should mean something that I am not able to figure out.

 

[erobz]

Good job. Thanks for finishing it out zee messy vay!

But it should mean something that I am not able to figure out.

As for the extraneous solution, I'm not concerned because temporally it makes sense to exclude the positive root solution of $u$, because the solution corresponding to the negative root $u$ must be the first collision temporally (if there were indeed two).

If it were the other way around and we found the solution corresponding to the positive root (coming after the other solution in time), I would be concerned...

 

[brotherbobby]

Glad the thread remains open. I had a question for @PeroK, if you're here.

In post# 9, you said that

The symmetry (of free fall - my addition) is inherent in the equations of motion

I am trying to investigate the matter but I am stuck somewhere I want to tell you about. Let me begin simply.

$(1)$. If an object is thrown vertically up, the time of rise = time of fall as well we the initial velocity of projection = final velocity. [I can prove both of these - they are elementary].

$(2)$. From (1) above, we can show that the time to climb to a height $y$ = time to fall from the height $y$ to the ground, even though at the height $y$ the ball has a finite speed. [Contrast with (1) where the speed at the highest point is 0].

$(3)$. Is it also true that for a ball thrown vertically up and which rises to a maximum height $h$, the time to scale a height $y$ is the same as the time that the ball dropped from the height $h$ will take to fall a distance $y$ down?

[ I cannot show $(3)$ either using symmetry arguments or algebra using the kinematic equations ].

Many thanks.

 

[PeroK]

$(3)$. Is it also true that for a ball thrown vertically up and which rises to a maximum height $h$, the time to scale a height $y$ is the same as the time that the ball dropped from the height $h$ will take to fall a distance $y$ down?

[ I cannot show $(3)$ either using symmetry arguments or algebra using the kinematic equations ].

Many thanks.

That can't be the same because the initials speeds are different.

For an elastic ball, the time to fall from height $h$ is the same as the time to bounce back up to height $h$.

First, we have the same acceleration due to gravity, $g$. Second, we have the same distance. Third, we have the same final speed in the first case as the initial speed in the second case.

This implies that the initial speed in the first case (speed at height $h$) is the same as the final speed in the second case (also height $h$). This can also be seen directly from conservation of mechanical energy. Note that conservation of energy also covers the case of a varying gravitational force/potential.

For constant acceleration, you can use the kinematic equations to show that the time is the same up and down.