Determining How To Measure Position Langrange's Equation

[embphysics]

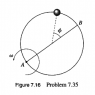
Figure 7.16 is a bird's-eye view of a smooth horizontal wire hoop that is forced to rotate at a
fixed angular velocity co about a vertical axis through the point A. A bead of mass m is threaded on the hoop and is free to move around it, with its position specified by the angle \phi that it makes at the center with the diameter AB. Find the Lagrangian for this system using as your generalized coordinate. (Read the hint in Problem 7.29.) Use the Lagrange equation of motion to show that the bead oscillates about the point B exactly like a simple pendulum. What is the frequency of these oscillations if their amplitude is small?

I am sort of confused as to exactly what the motion is. Does the hoop rotate around the point A, and does this hoop then exert some force on the bead, causing it to rotate through angles around the loop, the angles being measured relative to the fixed point B? If this is true, is there someway of relating the angular velocity of the loop to the angular velocity of the bead?

 

[UltrafastPED]

It would be easier if you attached figure 7.16.

 

[embphysics]

Hmm, I distinctly remember attaching the figure. Let me try this again.

 

[UltrafastPED]

Yes, the hoop is "hinged" at point A, and the axis AB swings around point A with a fixed frequency, ω.

The hoop has a diameter D = length of AB. The bead has mass m and can be located by the angle it makes with the axis AB, with the angle θ being used to track it ... say it runs CCW with zero the line AB, with B at 12 o'clock.

We need a second angle to describe the hoop's position ... let vertical be 12 o'clock, and let ψ run CCW.

Then the bead is located in space by the angles θ,ψ.

 

[embphysics]

Now, is there a way we can write θ in terms of ψ, or ψ in terms of θ?

 

[UltrafastPED]

The geometry of the system does not provide any relationship - they are independent.

There will be dynamical relationships (depending upon starting values and time); for these you must find the equations of motion.

 

[embphysics]

Okay. So, do I need to consider the kinetic energy of the bead and hoop, or just the bead? And would this system have potential energy, wouldn't it be zero?

 

[UltrafastPED]

The mass of the hoop is not given, and it's motion is uniform (forced by some engine) - so only the bead's energy is required.

So pick some inertial reference frame (like when the hoop is vertical, ψ=0, and establish the kinetic energy of the bead in terms of the angle θ: this will include the tangential motion along the hoop, as well as the rotational energy from the motion of the hoop; this latter will depend on the angle θ due to the changing effective radius of this rotation. The angular velocity in this direction is fixed: ω.

The potential energy will be due to gravity, and for this you will need both angles.

 

[embphysics]

Is this hoop vertical? From the context of the question, and the pictures, I figured the hoop and bead lay in the horizontal plane. If this is the case, how does gravity effect either the bead or hoop?

 

[UltrafastPED]

You are correct ... the hoop rotates about a vertical axis; thus there is no gravity.

 

[embphysics]

Okay, let me summarize what I think is going on, even though I might be repeating myself. As the hoop rotates around the point A, the bead will rotate around the hoop, having an angular position of \phi (t) relative to the line AB; \dot{\phi}(t) will be it's angular velocity relative to this line. So, it's angular velocity relative to just the point A, that is, its angular velocity relative to the vertical axis going through the point A, will be \psi = \dot{\phi} + \omega. As the hoop rotates around the point A, the bead will rotates around the hoop, causing the distance between the bead and the point A to vary, which I imagine would result in its rotational inertia and rotational KE to vary.

So, the KE would be KE = \frac{1}{2}mv^2 + \frac{1}{2}I \psi^2, where v is the tangential velocity of the bead? Does this seem correct?

 

[UltrafastPED]

Seems OK!