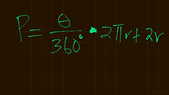SUMMARY
The correct formula for calculating the perimeter of a sector with a radius of 5 inches and an angle of 30° is P = (30/360) • (2π)(5) + 2(5), which results in a perimeter of 12.62 inches. The initial computation of P = 10.05 inches was incorrect due to a misapplication of the formula. The angle must be converted to radians correctly, where 30° is equivalent to 30 • (π/180). This discussion clarifies the proper method for calculating the perimeter of a sector.
PREREQUISITES
- Understanding of sector geometry
- Familiarity with the formula for perimeter of a sector
- Knowledge of angle conversion from degrees to radians
- Basic proficiency in using π in calculations
NEXT STEPS
- Study the formula for the perimeter of a sector in detail
- Practice converting angles from degrees to radians
- Explore additional examples of sector perimeter calculations
- Learn about the properties of circles and sectors in geometry
USEFUL FOR
Students studying geometry, educators teaching mathematical concepts, and anyone interested in mastering calculations involving sectors and circles.