Difference between time / length equations for time dilation

[Pochen Liu]

Homework Statement

What makes an event and when do I apply each equation to their respective situations

Relevant Equations

*attached

What is the difference between time dilation (t is the stationary reference frame)
t =

Description:
If two successive events occur at the same place in an inertial reference frame, the time interval 􏰋t0 between them, measured on a single clock

And this equation for time, if we take t' as the moving reference frame.

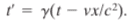
Description:
Relate the spacetime coordinates of a single event as seen by observers in two inertial frames, S and S' In terms of events, because I'm now confused as what classifies as an event. If you could provide a distinct example of when to use either equation that would be so helpful!

 

[phinds]

An event is simply a single point in space-time. Note that this is NOT a single point in space and it is NOT a single point in time.

Also be aware that the terminology "moving frame of reference" should NOT be used since it leads to confusion. Frames of reference don't move, objects do.