MisterH
- 12
- 0
This is about signal processing, moving averages & superposed / standing waves. This is an online system: causal (univariate) time series analysis.
Suppose you have a sinusoid of period n (i.e. n=40, so its frequency is 0.025). If you calculate a "weighted moving average" (WMA) on this sinusoid with a lookback-window equal to 1/4th the period of the sinusoid (i.e. 40/4 = 10), and from this WMA, you subtract an "exponential moving average" (EMA) with an alpha equal to 1 divided by 1/4th the period of the sinusoid (i.e. 1/10 = EMA alpha of 0.1), the resulting difference is perfectly "in phase" with the sinusoid. But this is only true if you do it for the n/4 setting. In fact, the result looks a lot like a superposed, standing wave: like in this image:
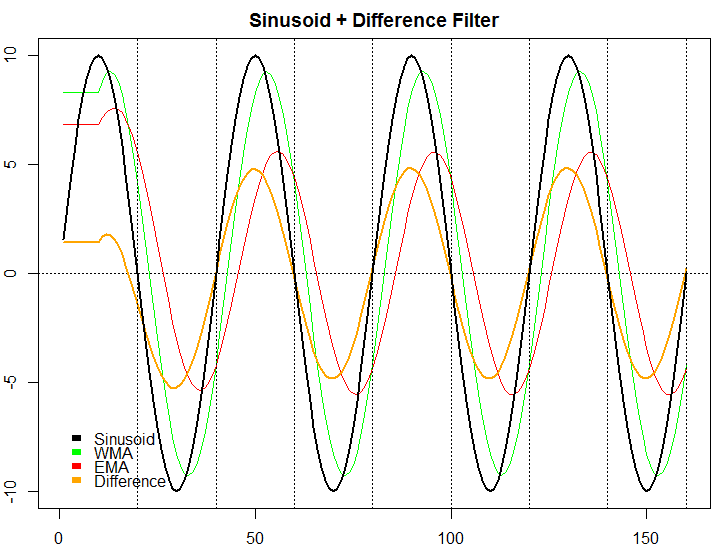
This cannot be a coincidence. There must be some kind of "deeper" reason that I fail to understand: why is this only true, if you pick n/4 for the WMA, and its equivalent for the EMA, and if you compare this exact difference (WMA-EMA) with the input wave signal, they are exactly in-phase: they turn at the same moment, and reach 0 at the same moment in time. There is no phase difference. Why?
Could it be related to the fact that a sine wave is made up of 4 identical pieces? (mirrored and inverted)?
Or something about the sine & cosine and the unit circle?
Or is it related to the lag / group delay of the WMA and EMA filters?
Or to the fact that this difference (WMA-EMA) has negative filter weights (not common in causal time series analysis)?
Why o why is this so.. I just know it's not a coincidence, there is a real explanation to this. Please help me because this intrigues me :) Thanks!
Suppose you have a sinusoid of period n (i.e. n=40, so its frequency is 0.025). If you calculate a "weighted moving average" (WMA) on this sinusoid with a lookback-window equal to 1/4th the period of the sinusoid (i.e. 40/4 = 10), and from this WMA, you subtract an "exponential moving average" (EMA) with an alpha equal to 1 divided by 1/4th the period of the sinusoid (i.e. 1/10 = EMA alpha of 0.1), the resulting difference is perfectly "in phase" with the sinusoid. But this is only true if you do it for the n/4 setting. In fact, the result looks a lot like a superposed, standing wave: like in this image:
This cannot be a coincidence. There must be some kind of "deeper" reason that I fail to understand: why is this only true, if you pick n/4 for the WMA, and its equivalent for the EMA, and if you compare this exact difference (WMA-EMA) with the input wave signal, they are exactly in-phase: they turn at the same moment, and reach 0 at the same moment in time. There is no phase difference. Why?
Could it be related to the fact that a sine wave is made up of 4 identical pieces? (mirrored and inverted)?
Or something about the sine & cosine and the unit circle?
Or is it related to the lag / group delay of the WMA and EMA filters?
Or to the fact that this difference (WMA-EMA) has negative filter weights (not common in causal time series analysis)?
Why o why is this so.. I just know it's not a coincidence, there is a real explanation to this. Please help me because this intrigues me :) Thanks!