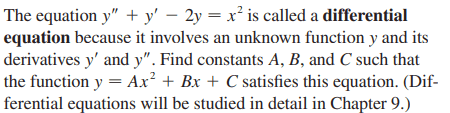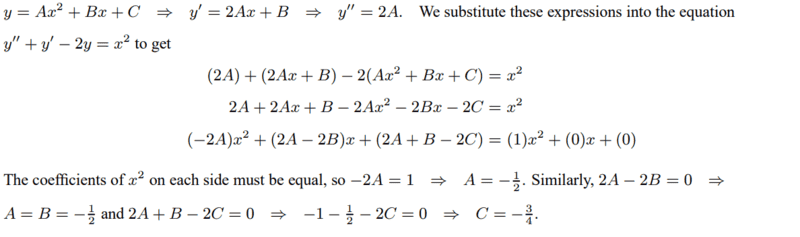WWGD said:
When would nullity be infinite-dimensional in a finite order ODE?
Edit: or maybe you mean## C^2(\mathbb R)##?
Proving that the solution space is a finite dimension affine space (that's embedded in a finite dimension vector space), so that you can translate the problem to a problem in linear algebra, you'd need to know beforehand that the differential operator is of finite nullity, which will intuitive is not (?) entirely obvious. [Maybe you'd know how to translate this into a linear matrix differential equation Y' = AY + C, in which case it will be somewhat obvious]
This at first hand does not seem like linear algebra would be enough to solve it, after all most of the results of linear algebra hinge on the fact that we work on finite dimensional vector spaces. HOWEVER, the following nullity theorem:
$$\dim(\ker(AB)) \leq \dim(\ker(A)) + \dim(\ker(B))$$
Works even for infinite dimensions, though it's mostly useless if the linear operators don't have finite nullity (dim ker).
Plus the fact that you can manipulate it to prove a solution ##y## must be ##C^\infty## and thus the derivative is an endomorphism (linear transform onto the same vector space). This allows you to use the fundamental theorem of algebra, since as a ring the operator algebra generated by the derivative is going to be isomorphic to the ring of polynomials with complex coefficients, and split a differential operator into a product of linear differential operators and prove that it is in fact also finite nullity. (And in particular you can find the exact kernel by splitting the differential operator into distinct powers of linear terms. And whose kernels are always distinct so the kernel of the composition is just the direct sum of all the kernels of the distinct powers).
In particular if the equation is of the form ##p(D)y = z## and there exists a differential operator ##q(D)## with ##q(D)z =0## you have that ##y \in \ker(q(D)p(D))## which is finite dimensional. And much easier, to calculate a particular solution ##y_0## will be in a space that's isomorphic to ##\ker(q(D)p(D))/\ker(p(D))## (this avoids what physicists may call resonance) and the problem naturally translates into a matrix equation of the form ##Ax = b##.
In practice one doesn't do all of this, you just decompose the polynomial, find a good basis for the embedding space (usually the best ones are given by monomials of the form ##e^{ax} \cdot {x^k \over k!}##), remove the basis elements that are in the basis of the kernel ##\ker(p(D))##, write a matrix form for the derivative operator restricted to this space (technically the operator which makes a certain diagram commute, but this is a physics forum) and finish writing the matrix equation ##Ax = b##. This is probably much easier done than said, this is also much easier for computing several solutions for similar problems ##p(D)y = w## where ##w## also satsifies ##q(D)w = 0## is immediately translated into some ##Ax = c## after writing ##w## as a sum of the basis elements.