fanttamdiv
- 5
- 0
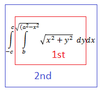
I am getting a different answer from my colleague on the double integral below so I am trying to find out why. I am trying to put this into excel so I can play with the numbers and see the different results. The double integral is below:
View attachment 1496
So the first integration (with respect to y) yields me this:
\[\int_{-c}^{c}\frac{(x^2*\sinh^{-1}{\frac{\sqrt{a^2-x^2}}{x}})-(b*\sqrt{x^2+b^2})+(a*\sqrt{a^2-x^2})-(x^2*\sinh^{-1}{\frac{b}{x}})}{2} dx\]
(Online calc input):
(.5)*(((x^2)*(arsinh((sqrt((a^2)-(x^2)))/x)))-(b*(sqrt((x^2)+(b^2))))+(a*(sqrt((a^2)-(x^2))))-((x^2)*(arsinh(b/x))))
Remember, I am putting this through excel so I am keeping the variables in there until the end. The second integration (with respect to x now) yields me this:
\[\frac{(-b^3*\sinh^{-1}{\frac{c}{b}})+(a^3*\sin^{-1}\frac{c}{a})-(bc*\sqrt{c^2+b^2})+(ac*\sqrt{a^2-c^2})}{2}\]
(Online calc input):
.5*(((-b^3)*(arsinh(c/b)))+((a^3)*(arcsin(c/a)))-((b*c)*(sqrt((c^2)+(b^2))))+((a*c)*(sqrt((a^2)-(c^2)))))
So now that I have this, I can use excel to plug in various variables and see how they affect my answer. The current variables I am using are:
a: 2
b: 1.2
c: 1
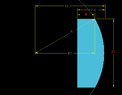
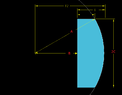
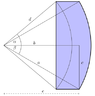
With the variables above, I am getting ~2.234. My colleague, however, is getting ~2.361. I do not have access to his work, and he seems confident in his answer (his answer makes more sense to me too based on some other details I haven't explained here). Basically I am bringing up this issue a couple years after he did the original problems and he isn't allotted any more time to work on this so I'm on my own. Is there something I am doing wrong? I don't think it is a rounding error as I have gotten the same answer with Excel and an online integration calculator. Also, I have tried to get this question answered on a different forum and it was suggested that I convert the integral to polar coordinates. It's been way too long since I took calculus and I don't know how to do this... Anyone think they can help do this/figure out why I'm getting a different answer?
Thanks
View attachment 1496
So the first integration (with respect to y) yields me this:
\[\int_{-c}^{c}\frac{(x^2*\sinh^{-1}{\frac{\sqrt{a^2-x^2}}{x}})-(b*\sqrt{x^2+b^2})+(a*\sqrt{a^2-x^2})-(x^2*\sinh^{-1}{\frac{b}{x}})}{2} dx\]
(Online calc input):
(.5)*(((x^2)*(arsinh((sqrt((a^2)-(x^2)))/x)))-(b*(sqrt((x^2)+(b^2))))+(a*(sqrt((a^2)-(x^2))))-((x^2)*(arsinh(b/x))))
Remember, I am putting this through excel so I am keeping the variables in there until the end. The second integration (with respect to x now) yields me this:
\[\frac{(-b^3*\sinh^{-1}{\frac{c}{b}})+(a^3*\sin^{-1}\frac{c}{a})-(bc*\sqrt{c^2+b^2})+(ac*\sqrt{a^2-c^2})}{2}\]
(Online calc input):
.5*(((-b^3)*(arsinh(c/b)))+((a^3)*(arcsin(c/a)))-((b*c)*(sqrt((c^2)+(b^2))))+((a*c)*(sqrt((a^2)-(c^2)))))
So now that I have this, I can use excel to plug in various variables and see how they affect my answer. The current variables I am using are:
a: 2
b: 1.2
c: 1
With the variables above, I am getting ~2.234. My colleague, however, is getting ~2.361. I do not have access to his work, and he seems confident in his answer (his answer makes more sense to me too based on some other details I haven't explained here). Basically I am bringing up this issue a couple years after he did the original problems and he isn't allotted any more time to work on this so I'm on my own. Is there something I am doing wrong? I don't think it is a rounding error as I have gotten the same answer with Excel and an online integration calculator. Also, I have tried to get this question answered on a different forum and it was suggested that I convert the integral to polar coordinates. It's been way too long since I took calculus and I don't know how to do this... Anyone think they can help do this/figure out why I'm getting a different answer?
Thanks