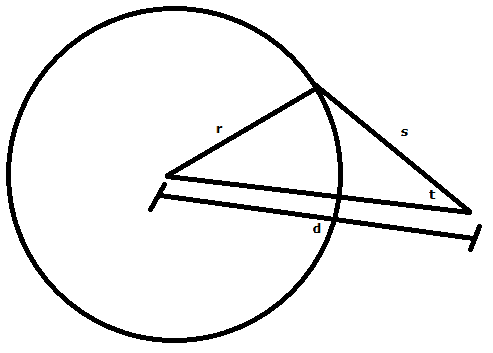SUMMARY
The discussion centers on finding the length \( s \) between a planet and a vessel using trigonometric principles, specifically the Law of Cosines and the Law of Sines. Participants suggest that while the Law of Cosines requires two sides and an included angle, the Law of Sines can be employed to derive the necessary angles and subsequently calculate \( s \). The quadratic formula is recommended for isolating variables when manipulating the equations. The conversation concludes with a consensus that using the Law of Sines may simplify the problem-solving process.
PREREQUISITES
- Understanding of the Law of Cosines
- Familiarity with the Law of Sines
- Basic knowledge of trigonometric identities
- Ability to solve quadratic equations
NEXT STEPS
- Study the Law of Sines in detail to apply it effectively in trigonometric problems
- Learn how to manipulate quadratic equations using the quadratic formula
- Explore trigonometric identities and their applications in solving triangles
- Investigate practical applications of trigonometry in physics, particularly in collision problems
USEFUL FOR
Mathematicians, physicists, engineers, and anyone involved in solving trigonometric problems related to distance and angles in physical scenarios.