Distance between two nucleons

[crick]

The potential energy associated to the interaction between nucleons has its minimum (point of equilibrium) at $r\sim 0.7 fm$, as showed in the following graph:

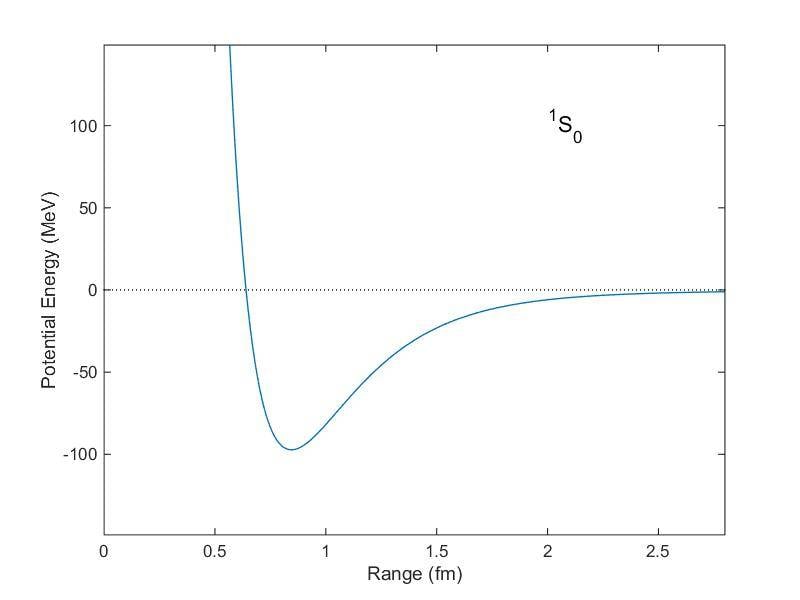
Nevertheless, there are two facts that are, apparently, in contrast with this:

- The average distance between nucleons is $\sim 1-2 fm$
- The average nucleon density is $\sim 0.17\,\,\ \mathrm{nucleons /fm^3}$

(These two are related because from the second follows a volume of $\sim 6 fm^2$ per nucleon which is in agreement with the average distance between nucleons)

So why is the average distance between nucleons usually greater that the $0.7 fm$ where the potential energy is minimum?

I'm aware that the "dimension" of nucleon is $\sim 1 fm$. But is this the reason why the distance between two of them cannot be much less?

 

[Orodruin]

The Coulomb potential has its minimum at $r = 0$, this does not mean that the average distance of the electron in a hydrogen atom is zero. There is no a priori reason to believe that the potential minimum should be at the same location as the average distance. There are more things that affect this.