Discussion Overview
The discussion revolves around the concept of distance traveled by a rocket moving at high speed between two stationary planets, specifically whether the distance is D or D*sqrt(1-(v/c)^2). Participants explore this question through different frames of reference, including the rocket's rest frame and the planets' rest frame, and engage in a detailed examination of relativistic effects on distance measurement.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
- Some participants propose that the distance traveled by the rocket in its own rest frame is zero, while others argue that it measures a distance of D*sqrt(1-(v/c)^2) in the frame of the rocket.
- A participant questions the frame of reference for measuring distance, suggesting that the distance could differ based on the observer's frame.
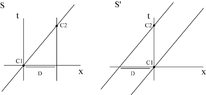
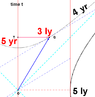
- It is noted that in the frame of the planets, the distance between them remains D, while in the rocket's frame, it is contracted to D*sqrt(1-(v/c)^2).
- Some participants discuss the implications of length contraction and the relativity of simultaneity, highlighting that different observers may measure different distances for the same physical scenario.
- A spacetime diagram is referenced to illustrate the differences in measured distances from various frames of reference.
- There is mention of the "pole-barn paradox" as a relevant thought experiment to understand the implications of length contraction and simultaneity.
Areas of Agreement / Disagreement
Participants express multiple competing views regarding the distances measured in different frames, and the discussion remains unresolved on certain aspects, particularly regarding the interpretation of distances in relation to length contraction and simultaneity.
Contextual Notes
Limitations include the dependence on the definitions of distance and simultaneity in different frames, as well as unresolved mathematical steps in the transformation between frames.