Divergence/Convergence for Telescoping series

In summary, the divergence test can be used on the partial sum of a telescoping series. If the limit of the nth term does not equal 0 as n approaches infinity, then the series diverges. In order to determine the convergence or divergence of a telescoping series, one must examine the convergence of the sequence of terms that make up the series.
  • #1
Neon32
68
1
Can I use the divergence test on the partial sum of the telescoping series?
Lim n>infinity an if not equal zero then it diverges

The example below shows a telescoping series then I found the partial sum and took the limit of it. My question is shouldn't the solution be divergent? Since the result -1+cos 1 is not equal to 0? I'm confused.

upload_2017-3-25_11-45-47.png
 
Physics news on Phys.org
  • #2
that is right i guess
 
  • #3
Neon32 said:
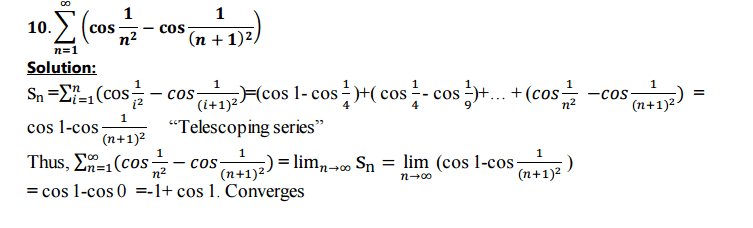
Lim n>infinity an if not equal zero then it diverges
it is ##a_n## must tend to zero, not the sum :)
 
  • #4
zwierz said:
it is ##a_n## must tend to zero, not the sum :)

what's ##a_n##?
 
  • #5
a term of the series
 
  • #6
zwierz said:
a term of the series

How can I determine convergence/divergence for telescopinc series then?
 
  • #7
you have already done this
 
  • #8
zwierz said:
you have already done this
I haven't? the solution is above, however I don't quite understand. I want a general rule to detect convergence/divergence fore telescoping series.
 
  • #9
The series ##\sum (b_{n+1}-b_n)## is convergent iff the sequence ##b_n## is convergent
 
  • #10
zwierz said:
The series ##\sum (b_{n+1}-b_n)## is convergent iff the sequence ##b_n## is convergent
but he didn't find the convergence of bn sepeartly in the solution above?
 
  • #11
He restored the proof of my proposition for this concrete example
 

1. What is a telescoping series?

A telescoping series is a type of infinite series in which most of the terms cancel each other out, leaving only a finite number of terms to be summed.

2. How can I determine if a telescoping series converges or diverges?

To determine convergence or divergence of a telescoping series, you can use the telescoping property of the series. If the limit of the partial sums of the series exists and is finite, then the series converges. If the limit does not exist or is infinite, then the series diverges.

3. What is the telescoping property of a series?

The telescoping property of a series states that if the terms of a series can be expressed as the difference of two consecutive terms, then most of the terms will cancel out when the series is summed, leaving only a finite number of terms.

4. What is a partial sum of a telescoping series?

A partial sum of a telescoping series is the sum of a finite number of terms in the series. It is used to determine the convergence or divergence of the series.

5. Can a telescoping series diverge even if its terms approach zero?

Yes, a telescoping series can still diverge even if its terms approach zero. This is because the terms may not cancel out completely, resulting in a non-zero value for the sum of the series.

Similar threads

B Understanding about Sequences and Series
    • Calculus
Replies
3
Views
946
B Difficulty with understanding whether 1/n converges or diverges
    • Calculus
Replies
11
Views
2K
I Understanding the nth-term test for Divergence
    • Calculus
Replies
15
Views
2K
I How does the ratio test fail and the root test succeed here?
    • Calculus
Replies
6
Views
685
MHB Power Series (Which test can i use to determine divergence at the end points)
    • Calculus
Replies
1
Views
1K
I Testing for Divergence using the Integral Test
    • Calculus
Replies
1
Views
1K
MHB Does the Comparison Test Determine Convergence or Divergence of Series?
    • Calculus
Replies
3
Views
937
MHB Use the techniques of geometric series
    • Calculus
Replies
4
Views
2K
MHB 11.6.8 determine convergent or divergence by Ratio Test
    • Calculus
Replies
3
Views
915
I Taming a Divergent Series -- But how does it work?
    • Calculus
Replies
14
Views
2K

Hot Threads

Recent Insights

Back
Top