Does a photon travel freely through the CMB photon gas?

[JimJCW]

A photon often travels billions of years (Gyr) through the CMB photon gas (410 photons per cubic centimeter) to reach us. Does it travel freely? Let’s share our thoughts about this.

For discussion purpose, let’s assume the photon has a wavelength of 500 nm, close to the peak of the solar spectrum. During a journey of 1 Gly, for example, the number of CMB photons coming within a wavelength of the traveling photon is estimated to be,

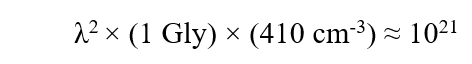
This is a large number.

Because of the linearity of the classical Maxwell equations, it is generally assumed that the traveling photon does not interact with the CMB photons. However, the theory of quantum electrodynamics opens the possibility of photon-photon scattering via virtual electron-positron pairs in vacuum (see, for example, Two-photon physics).

Does the photon travel freely? If not, over a long distance/time, even a slight interaction might accumulate a significant effect.

 

[Vanadium 50]

Put some numbers in that and see if it is plausible. (Hint: it's not)

 

[JimJCW]

Put some numbers in that and see if it is plausible. (Hint: it's not)

It seems that you already know the answer and know how to get it. Please share with us.

 

[PeterDonis]

It seems that you already know the answer and know how to get it. Please share with us.

No, you already know how to get the answer; you said so in your OP. Just calculate the amplitude for photon-photon scattering via virtual electron-positron pairs in vacuum, for photons with energy typical of CMB photons.

over a long distance/time, even a slight interaction might accumulate a significant effect.

There is no "might" necessary here. You have already given the method for calculating the effect; once you have the amplitude referred to above, just sum it over the time since recombination to see what the cumulative effect is.

You might also check the literature to see if someone else has already done this calculation (or something equivalent to it).

 

[JimJCW]

There is no "might" necessary here. You have already given the method for calculating the effect; once you have the amplitude referred to above, just sum it over the time since recombination to see what the cumulative effect is.

You might also check the literature to see if someone else has already done this calculation (or something equivalent to it).

The calculations involve Feynman box diagrams and are beyond my capability. Not many photon-photon scattering calculations have been reported. The one by Kanda (2011) gives a (1 eV)-(1 eV) scattering cross-section as,

https://www.physicsforums.com/attachments/288292

In our present case, for a 500 nm photon traveling through the CMB photon gas we need information of, for example, the cross-section of a (2.48 eV)-(0.000634 eV) scattering.

I think the reason not many photon-photon scattering calculations have been reported is that the effects are almost impossible to detect in the laboratory. In space, however, over a long distance/time and involving so many encounters, the interaction might accumulate a significant effect.

The Big Bang model assumes that there is no interaction between the traveling photon and the CMB photon gas, and the energy of the photon is affected only by space expansion, as indicated by the equation z+1 = 1/a, where a is the scale factor.

 

[JimJCW]

The calculations involve Feynman box diagrams and are beyond my capability. Not many photon-photon scattering calculations have been reported. The one by Kanda (2011) gives a (1 eV)-(1 eV) scattering cross-section as,

https://www.physicsforums.com/attachments/288292

In our present case, for a 500 nm photon traveling through the CMB photon gas we need information of, for example, the cross-section of a (2.48 eV)-(0.000634 eV) scattering.

I am sorry. For some reason the image did not show up. Here it is,

 

[Vanadium 50]

1. It is not true that these calculations are hard to find. It's in Jackson.
2. The Kanda paper cannot possibly be correct, as the electron mass does not appear. This is a factor of (ω/m)⁸. This may be why it has spent a decade as a preprint without being published.
3. Dimensional analysis alone suggests that the mean free path for a photon on energy E be of order \frac{m^8 \beta^6}{\alpha^4 E^3}.

where β is thermodynamic β. This works out to more than 10⁴² times the radius of the universe.

 

[Vanadium 50]

It seems that you already know the answer and know how to get it. Please share with us.

I find this attitude really irritating. Calculate this for me! Hop to it!

If you're not willing to put in the work to defend your idea, why is it my responsibility?

 

[berkeman]

Thread closed for Moderation.

 

[PeterDonis]

The calculations involve Feynman box diagrams and are beyond my capability.

Then you might as well accept what @Vanadium 50 is saying in post #7 (which looks correct to me), since you have no basis for questioning it. (Also, he gave you a reference, Jackson, in which you can find further information.)

 

[PeterDonis]

The OP question has been answered. Thread will remain closed.