Salman Ali
- 13
- 1
- TL;DR
- Which method easier to solve such questions which involve factorials?
So there are two parts of the question:
a) does the sequence converge or diverge
b) use nth term on the Series
Now sybomlab calculator is saying to apply ratio test!
a)
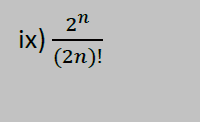
b)
So should I apply ratio test or is there any easy method? And what's the difference between these two questions and what methods differ?
a) does the sequence converge or diverge
b) use nth term on the Series
Now sybomlab calculator is saying to apply ratio test!
a)
b)
So should I apply ratio test or is there any easy method? And what's the difference between these two questions and what methods differ?
