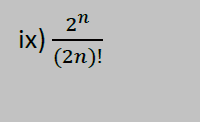Discussion Overview
The discussion revolves around determining whether the sequence defined by the expression (2^n)/(2n) converges or diverges, as well as the application of the nth term test on the corresponding series. Participants explore various methods for analyzing convergence, including the ratio test and the nth term test, while seeking clarification on the differences between the two questions posed.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Homework-related
Main Points Raised
- Some participants suggest applying the ratio test to determine convergence, while others question if there are easier methods available.
- One participant notes the importance of distinguishing between the convergence of the sequence and the convergence of the series formed by summing the sequence's terms.
- There is a discussion about the usefulness of the nth term test, with some participants indicating it is often not helpful for establishing convergence.
- Some participants express a need for clarification on how to solve both parts of the question, while others emphasize the necessity of demonstrating one's best effort before seeking help.
Areas of Agreement / Disagreement
Participants generally agree on the distinction between the convergence of the sequence and the series. However, there is no consensus on the best method to apply for determining convergence, as multiple approaches are discussed without a clear resolution.
Contextual Notes
Some participants mention the ratio test and nth term test, but there are unresolved questions regarding their applicability and effectiveness in this context. The discussion reflects varying levels of understanding and comfort with these concepts.
Who May Find This Useful
This discussion may be useful for students studying sequences and series in calculus, particularly those grappling with convergence tests and their applications.