Discussion Overview
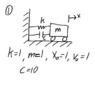
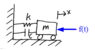
The discussion revolves around the existence of a transfer function for an unforced system, specifically in the context of a mass-spring-damper system. Participants explore the definitions and implications of transfer functions in scenarios where no external input is applied, examining both theoretical and practical aspects.
Discussion Character
- Debate/contested
- Conceptual clarification
- Technical explanation
Main Points Raised
- Some participants question whether a transfer function can exist without an actual input, noting that the standard definition involves output/input ratios.
- Others argue that the transfer function can be defined based on system properties, independent of current inputs, suggesting it describes potential system responses.
- One participant emphasizes that while the transfer function conceptually exists, it cannot be calculated without specifying an input.
- There is mention of the need for clear definitions regarding where inputs and outputs are applied in the system to properly determine the transfer function.
- Some participants propose that the transfer function can be derived from the system's differential equation, even if the system is not currently excited.
- Discussions include hypothetical inputs and the implications of defining transfer functions in the absence of explicit driving forces.
Areas of Agreement / Disagreement
Participants express differing views on the applicability of transfer functions to unforced systems. While some assert that transfer functions exist independently of inputs, others contend that the lack of a defined input makes the concept less applicable. The discussion remains unresolved with multiple competing perspectives.
Contextual Notes
The discussion highlights limitations in the problem statement, particularly the absence of specified inputs and outputs, which complicates the determination of the transfer function. Participants note that assumptions about inputs and outputs are necessary for a complete analysis.