Doubt about vector acceleration

[LCSphysicist]

Homework Statement

All below

Relevant Equations

All below

Say... A ball is moving to the right, and we want to say that it doesn't slip.

My doubt is, in which case we put
Vrot = - Vcm = - α*r
or
Vrot = Vcm = α * r

 

[etotheipi]

Consider a point P on the rigid body. The position vector of the point P, $\vec{r}_P$, is the sum of the position vector of the centre of mass $\vec{R}$ and the position vector from the centre of mass to P, $\vec{r}_P'$: $$\vec{r}_P = \vec{R} + \vec{r}_{P}'$$Taking the time derivative, $$\vec{v}_P = \vec{V} + \vec{v}_P'$$Now $\vec{v}_P'$ is the velocity P w.r.t. the centre of mass. If the angular velocity of the rigid body is $\vec{\omega}$, then any two points on the rigid body rotate about each other at angular velocity $\vec{\omega}$. So $\vec{v}_P' = \vec{\omega} \times \vec{r}_{P}'$.

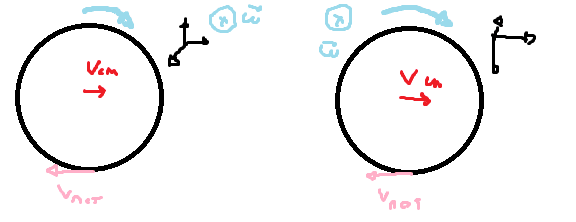
Now let's relate this to a rolling ball. Let $P$ be the point that is instantaneously at rest at the ball/ground interface, so $\vec{v}_P = \vec{0}$. If the $\hat{x}$, $\hat{y}$ and $\hat{z}$ axes point right, up and into the page respectively, then you have $$\vec{0} = \vec{V} + \omega_z \hat{z} \times (-r)\hat{y} = \vec{V} - \omega_z r \hat{x} = (V_x - \omega_z r)\hat{x}$$And this means that $V_x = \omega_z r$, which is the rolling condition.

But we could have just as easily taken the $\hat{z}$ axis to point out of the page, in which case that cross product flips sign, and also $\omega_z < 0$, and you would have $V_x = -\omega_z r$. So really both of your answers could be correct (but $\vec{\omega}$ instead of $\vec{\alpha}$), it depends how you define your coordinate system . Specifically, whether you're using a right-handed or left-handed basis.

 

[haruspex]

Homework Statement:: All below
Relevant Equations:: All below

Say... A ball is moving to the right, and we want to say that it doesn't slip.
View attachment 264964
My doubt is, in which case we put
Vrot = - Vcm = - α*r
or
Vrot = Vcm = α * r

How are you defining v_rot? Is it the velocity of the point of contact relative to the mass centre? I will assume so.

It's going to depend on your choice of sign convention and whether your variables are scalar or vector.

You have shown explicit directions in the diagram, so if you are using scalar variables then those define the positive directions for each variable independently: v_rot=v_cm=αr.

If using vectors, you ought to use the same coordinate system for all linear motion vectors (displacements, velocities..). The arrows in the diagram become irrelevant to the algebra. Since the point of contact is static you know $\vec v_{rot}+\vec v_{cm}=0$.
Rotational vectors are trickier. You need a handedness rule. With the right hand rule,

1. The right hand, curled fingers and thumb, is used to turn the rotation direction into a vector. If the disc is turning clockwise as you view it then the vector (thumb) points away from you.
2. To find the direction of a tangential velocity, the cross product puts the rotation first: $\vec v_t=\vec \omega\times\vec r$.
3. To find the result of a cross product, use the right hand with the index finger for the first vector and the middle for the second. The thumb indicates the result.

So for the point of contact relative to the centre, the rotation (index finger) points away from you, the displacement vector (middle finger) points down and the cross product (thumb) points to the left.

https://en.m.wikipedia.org/wiki/Right-hand_rule helps.

 

[LCSphysicist]

So, to see if i get.
If we are dealing with vectors that we don't know the direction, but know the final conditions, that is, don't slip, let's see a example.

This wheel are released from b, and is attached to a spring which unstretched length is L.
Initially it is slipping, until it mesh with the teeth on the ground

Say, about the point on contact which occurs the collision.
Lo = mrv {this are scalars}
Lf = mrvf + I*w

W in this case:

vf + vrot = 0
vf = -vrot = -wxr

And, because i assumed L positive outing of the paper,

W positive cross V positive would be (-wr)j, so
vf = -(-wr) = wr

Is this analyse right?

 

[etotheipi]

Looks alright; you take the origin of the coordinate system to be somewhere along the ground, and then the spring-wheel system is acted upon by zero external torques (the line of action of the friction force passes through the origin). So angular momentum of that system is conserved, $L_o = L_f$.

If you take the $\hat{z}$ axis to point out of the paper, then an anticlockwise angular velocity would indeed be positive, and you do have $v_f = \omega r$. Or in vector form, $\vec{v}_f = -\omega r \hat{x}$, if $\hat{x}$ points to the right.

Since $\vec{v}_f = -\vec{v}_{rot} = -\vec{\omega} \times \vec{r} = -(\omega \hat{z}) \times (-r\hat{y}) = -\omega r \hat{x}$

 

[haruspex]

you take the origin of the coordinate system to be somewhere along the ground, and then the spring-wheel system is acted upon by zero external torques

Perhaps it is a subtle distinction, but I would say it doesn’t matter where the origin of the coordinate system is. What matters is the reference axis for the torques and moments. Within one coordinate system you can express torques about different axes.

 

[etotheipi]

Perhaps it is a subtle distinction, but I would say it doesn’t matter where the origin of the coordinate system is. What matters is the reference axis for the torques and moments.

I would say that torques, angular momenta and the like are defined w.r.t. a coordinate system e.g, as $\vec{\tau} = \vec{r} \times \vec{F}$, or $\vec{L} = \vec{r} \times \vec{p}$. All of these require having picked a coordinate origin.

But we interpret the components of these rotational vectors as components of those quantities about a certain axis of our coordinate system. So $L_z$ would be the component of angular momentum about the $\hat{z}$ axis, etc.

So I would define a coordinate system with origin somewhere along the ground, and use the König theorem for angular momenta to write the angular momentum of the thing w.r.t. this coordinate system as $\vec{r}_{cm} \times M\vec{V}_{cm} + \tilde{I}\vec{\omega}$, where $\tilde{I}$ is the full MoI tensor at the centre of mass. That's quite unwieldy, though, so it makes sense to decompose the motion w.r.t. our Cartesian basis, e.g. by doing things like $\vec{\omega} = \omega \hat{z}$ and as such only needing to worry about $I_{zz}$ component in the MoI tensor (assuming the necessary symmetry to ignore the off-diagonal terms).

Putting the origin of the coordinate system along the ground means that $\vec{r} \times \vec{F}_{friction} = \vec{0}$, so we can consider the system closed for angular momentum. So I think it definitely does matter where the origin is .

 

[kuruman]

As you already know, a velocity is unambiguously defined when it is clear what frame of reference one is using. In post #1 you show a drawing where one arrow $v_{cm}$ represents the velocity of the center of mass relative to the surface on which the wheel is rolling and another arrow $v_{rot}$ represents the velocity of the point of contact with respect to the center of mass. For rolling without slipping, as shown in post #1, it is true that

1. In the CM frame $v_{cm}=0$ and $v_{rot}=\omega r$ to the left.
2. In the surface frame $v_{cm}=\omega r$ to the right and $v_{rot}=0$.

Now if you want to compare a velocity in one frame with a velocity in another frame, you must state explicitly the frame of reference for each velocity. For example, according to the information in statements 1 and 2 above, one might say "The velocity of the center of mass as measured in the surface frame is equal and opposite to the velocity of the contact point as measured in the CM frame and their magnitude is $\omega r$.

My own opinion is that mixing velocities relative to different frames of reference in one equation can lead to trouble and should be avoided.

 

[etotheipi]

2. In the surface frame $v_{cm}=\omega r$ to the right and $v_{rot}=0$.

That second part doesn't make too much sense to me. Specifically, I have no idea what $v_{rot}$ means in the lab frame.

In the lab frame we can measure the velocity of the centre of mass $v_{cm}$ and also the velocity of any point on the wheel e.g. $v = 0$ at the point of contact.

To me $\vec{v}_{rot} = \vec{\omega} \times \vec{r}$ if $\vec{\omega}$ is the angular velocity of the rigid body, which is relevant to body fixed frames of reference (or the non-rotating CM frame).

 

[kuruman]

That second part doesn't make too much sense to me. Specifically, I have no idea what $v_{rot}$ means in the lab frame.

In the lab frame we can measure the velocity of the centre of mass $v_{cm}$ and also the velocity of any point on the wheel e.g. $v = 0$ at the point of contact.

To me $\vec{v}_{rot} = \vec{\omega} \times \vec{r}$ if $\vec{\omega}$ is the angular velocity of the rigid body, which is relevant to body fixed frames of reference (or the non-rotating CM frame).

As defined in the drawings by OP in the original post, $v_{rot}$ is the velocity of the point on the rim that makes contact with the surface. In the surface frame and for rolling without slipping that point is instantaneously at rest. That's all.

 

[etotheipi]

As defined in the drawings by OP in the original post, $v_{rot}$ is the velocity of the point on the rim that makes contact with the surface. In the surface frame and for rolling without slipping that point is instantaneously at rest. That's all.

Ah okay, thanks for clarifying. I think in any case we're agreed on the Physics but are just calling the variables different things