Drag Forces and Terminal Velocity

[rosedog09]

Homework Statement

3. Describe how the mass of an object changes the terminal velocity of that object when falling.

5. A 79 kg Skydiver opens up her parachute and instantly decelerates at 8 m/s^2. Determine the Force of Air Resistance for this situation!

Relevant Equations

F = ma

Teacher says Im wrong on both these questions. I have consulted with other teachers and they say im correct. What do you guys think?


3. As mass increases, so does terminal velocity.

5. F_net = F_Drag - F_g
ma = F_Drag - mg
F_Drag = 79(8) + 79(10)
F_Drag = 632 + 790 = 1422 N

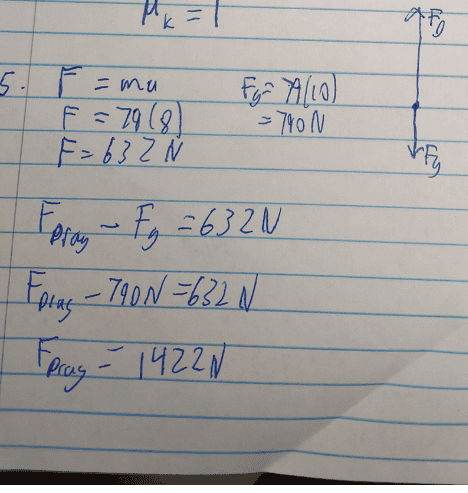
Teacher Comments

5 and 3 are incorrect

Teacher Clarification (Email)

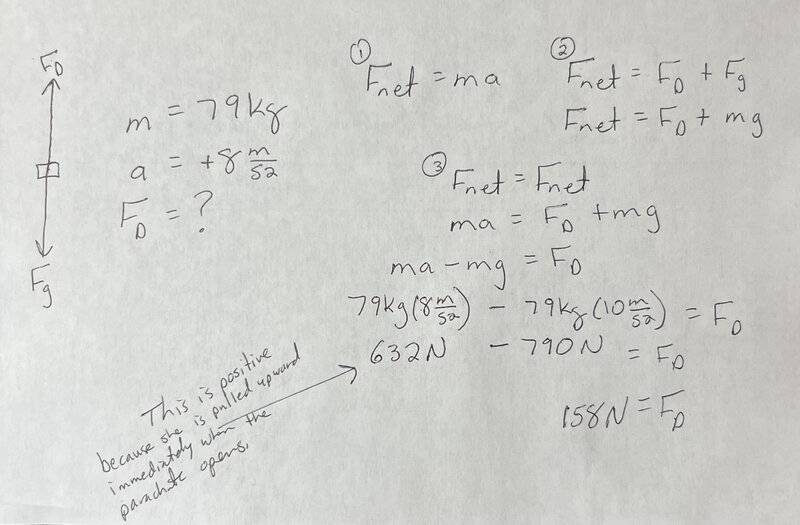
My Response :

Teacher Further Response

 

[kuruman]

You are correct. Your teacher seems to be confused about how Newton's second law works. From the diagram in the email and using the convention that "up" is positive, the net force is
$F_{net}=F_D-mg=F_D-79~(\text{kg})\times 9.8~(\text{m/s})^2.$
Mass times acceleration is positive (up)
$ma=79~(\text{kg})\times 8~(\text{m/s})^2.$
Newton's second law is
$F_{net}=ma$
Substitute
$F_D-79~(\text{kg})\times 9.8~(\text{m/s})^2=79~(\text{kg})\times 8~(\text{m/s})^2\implies F_D=79~(\text{kg})\times (8+9.8)~(\text{m/s})^2.$

 

[erobz]

On 3 you are incorrect correct. The terminal velocity ( asymptotically approached velocity for which $\dot v =0$ from Newtons Second) is inversely proportional to the mass or square root of it $( F_D \propto v^2)$

 

[rosedog09]

On 3 you are incorrect. The terminal velocity ( asymptotically approached velocity for which $\dot v =0$ from Newtons Second) is inversely proportional to the mass or square root of it $( F_D \propto v^2)$

 

[erobz]

View attachment 344059

My bad, you’re right. (Lesson for me) Don’t do mental manipulations on low sleep! Sorry.

 

[rosedog09]

My bad, you’re right. (Lesson for me) Don’t do mental manipulations on low sleep! Sorry.

All good. I can relate atm. All my AP exams are coming up and that doesn't stop my teachers from assigning lots of homework, so lots of late nights.

 

[erobz]

All good. I can relate atm. All my AP exams are coming up and that doesn't stop my teachers from assigning lots of homework, so lots of late nights.

I wish my sleepless nights were by choice. Good luck on the exams.

 

[haruspex]

To put @kuruman's explanation in a form that might be closer to the teacher's thinking…

$ma=F_{net}=F_D+F_g$
is correct provided all forces and accelerations will be filled in using the same sign convention .
$F_g=mg$ implies the sign convention is positive down (since g is always taken as a magnitude, so positive).
With that convention, $a=-8ms^{-2}$.
$F_D=-mg+ma=m(-10-8)ms^{-2}$.
But again, that is positive down, so the upward drag force is
$m(10+8)ms^{-2}$.

Moral: always state your sign conventions and check you have adhered to them.

 

[kuruman]

Moral: always state your sign conventions and check you have adhered to them.

I think that adherence to the sign convention is not the teacher's problem here but unrecognized self-contradiction is.
Teacher says
"There is an upward Force and a downward Force."
Furthermore, the diagram in the teacher's email shows the drag and weight forces in opposite directions. This is all true and correct.

Then in the next sentence the teacher says
"Drag Force and Force Weight act opposite the Force caused by the upward acceleration."
Whatever the direction of this so called force caused by the upward acceleration, the second statement implicitly contradicts the first by asserting that drag and weight act opposite to this force, i.e. drag and weight act in the same direction.

The sign convention whether "up" is positive or negative never enters the picture.