evinda
Gold Member
MHB
- 3,741
- 0
Hello! (Wave)
I want to draw trees, that traverse "MATHHELPBOARDS" in:
That's what I have tried:
Could you tell me if it is right or if I have done something wrong? (Thinking)
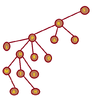
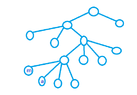
I want to draw trees, that traverse "MATHHELPBOARDS" in:
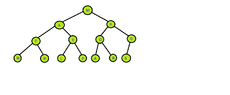
- pre-order
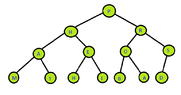
- in-order
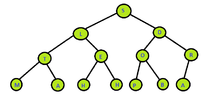
- post-order
That's what I have tried:
- pre-order
View attachment 3580
- in-order
View attachment 3581
- post-order
View attachment 3582
Could you tell me if it is right or if I have done something wrong? (Thinking)