Dynamic forces with radial acceleration

[trajan22]

well this problem is killing me and I've spent a good 3 hours or so on it and still have no real results.

This is the problem
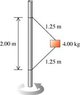
The 4.00-kg block in the figure View Figure is attached to a vertical rod by means of two strings. When the system rotates about the axis of the rod, the strings are extended as shown in the diagram and the tension in the upper string is 80.0 N.
What is the tension in the lower cord?

How many revolutions per minute does the system make?

there is the picture provided



what i did

i realized that the sum of the forces in the x direction is equal to Tsin(theta) and that this is equal to the mass times the radial acceleration
I bisected the triangle in order to make it a right triangle. from here i found the angle measures using arcsin(1/1.25)... i also found the radius by using the pythagorean thrm. to be .75m.
from here i tried to solve part b but came out with a wrong answer

for the y direction i know the sum of the forces is equal to cos(theta)+(-mg)
these forces that I've described are only for the top string and not the bottom...im not really sure where to go from here or if I am even on the right track

sorry to bother you guys again I am just on the verge of giving up on this problem

I think the main problem is that I am having troubel with finding all the forces for centripetal acceleration.
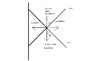
ive attached a force diagram that i made. but I am missing something??

 

[trajan22]

ive added a force diagram to this problem...but I am stilll utterly confused please help.

 

[big man]

You know that the vertical force from the upper cord is going to be T_1cos \theta. You also know that this needs to cancel the downwards force from the wieght of the block and the tension from the lower cord.

You are right in equating the sum horizontal parts of the tension forces to the centripetal force of \frac {mv^2} {r}, but you just made a mistake in your calculations of the radius.

Like you said use pythagoras's theorem.

Use c^2 = a^2 + b^2
you know that a=1 and c=1.25 so plug that into the equation above and rearrange to solve for b.

You can then solve for v using the method you were using before (paragraph 2) and then you just need to think of how you can get the number of revolutions per minute from knowing the velocity.

 

[trajan22]

well i still am not getting the right tension in the lower string though...i am taking Tcos(37) to be the normal force and i am subtracting the weight because it is providing slack to the lower string. where is this going wrong

 

[big man]

So is your equation for the vertical components this:

T_1 cos \theta_1 = T_2 cos \theta_2 + Mg

where \theta_1=\theta_2

That should give you the right answer. There is one upwards force, which is T_1 cos \theta and then there are two downwards forces, which are Mg and T_2 cos \theta. The only thing that could make it so you are getting the wrong answer is that \theta_2 is wrong...and that would mean that the diagram is wrong. Either that or the answer in the book is wrong.