Undergrad Eigenkets belonging to a range of eigenvalues

[Spin One]

When one wants to represent a general ket in a basis consisting of eigenkets each attributed to an eigenvalue in a range, say from a to b, why does one take the integral of said kets from a to b w.r.t. the eigenvalues?

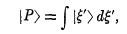
I understand that the integral here plays a role analogous to a sum in the case where a general ket is expressed in terms of eigenkets belonging to discrete eigenvalues, but I don't understand why each vector is multiplied by an infinitesimal change near the eigenvalue it belongs to. Interpreting this integral as the limit of a sum we get:
[P>=Σ[ξ>Δξ (lim.Δξ→0)
where I do not understand the role of Δξ.

 

[bhobba]

See the recently featured thread:
https://www.physicsforums.com/threa...ces-in-quantum-mechanics.917768/#post-6017221

Thanks
Bill

 

[stevendaryl]

I looked over the thread about Rigged Hilbert Spaces, and I'm not sure that it completely explained the relationship between continuous and discrete bases.

In a non-rigorous way, you can think of the continuous basis as a limiting case of the discrete basis. However, in going from discrete to continuous, the normalization convention for basis elements changes.

Let me illustrate. Suppose you have an operator $\Lambda$ with discrete eigenvalues $\lambda_j$. I think in order for the continuum limit to make sense int the most straightforward way, you need to assume that $\lambda_{j+1} > \lambda_j$, and that there are infinitely many $\lambda_j$, and that the corresponding eigenstates $|n\rangle$ form a complete orthonormal basis. That means that

1. If $n \neq m$, then $\langle n|m\rangle = 0$
2. $\langle n|n\rangle = 1$
3. If $|\psi\rangle$ is a properly normalized state, then $|\psi\rangle = \sum_n \langle n|\psi\rangle |n\rangle$
4. $\sum_n |\langle n|\psi\rangle|^2 = 1$

Now, if the coefficients $\langle n|\psi\rangle$ change slowly with $n$ (and maybe we also have to assume that $(\Delta \lambda)_n \equiv \lambda_{n+1} - \lambda_n$ remains bounded? I'm not sure...) then we can define a new ket with a different normalization:

$|\lambda_n\rangle \equiv \frac{1}{\sqrt{(\Delta \lambda)_n}} |n\rangle$

In terms of the $|\lambda_n\rangle$, we have:

$|\psi\rangle = \sum_n (\Delta \lambda)_n \langle \lambda_n |\psi\rangle |\lambda_n\rangle$

The kets $|\lambda_n\rangle$ have a different normalization:

• $\langle \lambda_n | \lambda_m \rangle = 0$ (if $m \neq n$)
• $\langle \lambda_n | \lambda_n \rangle = \frac{1}{(\Delta \lambda)_n}$

If the states $|\lambda_n\rangle$ change smoothly with $n$, then this can be approximated by an integral:

$|\psi\rangle = \int d\lambda \langle \lambda |\psi\rangle |\lambda\rangle$

 

[Spin One]

So dλ is introduced to make the product between each eigenket and dλ finite, since the eigenkets will be of "infinite length" in the sense of lim._Δλ→0[1/Δλ]. That makes sense. In that case, will the coefficients <λIΨ> be infinitesimal? Otherwise the integral would diverge, even over a finite range.

 

[bhobba]

So dλ is introduced to make the product between each eigenket and dλ finite, since the eigenkets will be of "infinite length" in the sense of lim._Δλ→0[1/Δλ]. That makes sense. In that case, will the coefficients <λIΨ> be infinitesimal? Otherwise the integral would diverge, even over a finite range.

Yes - but unless you want to get into non-standard analysis infinitesimals are a load of the proverbial, although used every now and then when speaking informally. I do it but shouldn't really.

There is no way to understand it properly unless you study the references in my link.

Start with Distribution Theory.

Thanks
Bill