Elastic collision, one object in circular motion

[azukibean]

Homework Statement

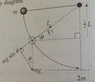
A steel ball of mass m is fastened to a cord of length L and released when the cord is horizontal. At the bottom of the path, the ball strikes a hard plastic block of mass M = 4m at rest on a frictionless surface. The collision is elastic.

Find the speed of the block immediately after the collision
Answer: (2/5)*\sqrt{}(2gL)

Homework Equations

KE + PE = KE + PE; (1/2)mv² + mgh = (1/2)mv'² + mgh'
m₁v₁ + m₂v₂ = m₁v'₁ + m₂v'₂

The Attempt at a Solution

COE
mgL = (1/2)mv²
v = √(2gL)

COM
mv₁ = mv'₁ + 4mv'₂
m√(2gL) = m(v'₁ + 4v'₂)
√(2gL) = v'₁ + 4v'₂
??

The textbook cites an example that wasn't even relevant. It said that the example was elastic and one object was at rest, but the example was actually the opposite.
It says v'₁ = v₁(m₁ - m₂)/(m₁ + m₂) and v'₂ = 2m₁/(m₁ + m₂). How can I prove this?
Also, in the diagram, it says m becomes 2m...?

 

[STEMucator]

It says v'1 = v1(m1 - m2)/(m1 + m2) and v'2 = 2m1/(m1 + m2). How can I prove this?

Consider two balls, one of mass $m_1$ and one of mass $m_2$. Suppose ball 1 is traveling at ball 2 with velocity $(v_{i_x})_1$ and strikes ball 2 in a perfectly elastic collision.

After the collision, the balls have velocity $(v_{f_x})_1$ and $(v_{f_x})_2$ respectively.

The collision must obey two conservation laws, namely the conservation of momentum (obeyed in any collision) and conservation of mechanical energy. The mechanical energy before and after the collision is purely kinetic.

Using the conservation of momentum and conservation of mechanical energy, along with some messy algebra, it can be proven both those equations hold.

 

[azukibean]

This is possibly one of the ugliest equations I've seen.
I can't set the two V_f1 equal to each other, that would lead to 0. But I also can't figure out where to go from there.

 

[STEMucator]

You have the two equations:

$m_1(v_{i_x})_1 = m_1(v_{f_x})_1 + m_2(v_{f_x})_2$ (1)

and

$\frac{1}{2} m_1(v_{i_x})_1^2 = \frac{1}{2} m_1(v_{f_x})_1^2 + \frac{1}{2} m_2(v_{f_x})_2^2$ (2)

In equation (1), start by isolating $(v_{f_x})_1$; call this equation (3). Then substitute the result into equation (2).

After some pain, you wind up with:

$(v_{f_x})_2 [(1 + \frac{m_2}{m_1})(v_{f_x})_2 - 2(v_{i_x})_1 ] = 0$

So either $(v_{f_x})_2 = 0$ or $[(1 + \frac{m_2}{m_1})(v_{f_x})_2 - 2(v_{i_x})_1 ] = 0$.

If $(v_{f_x})_2 = 0$, then ball 1 completely missed the other ball. So you want the other solution, which will give you a solution for $(v_{f_x})_2$. This solution happens to be one of your two equations.

To get the other equation, sub back $(v_{f_x})_2$ into equation (3), which will yield the other equation.

 

[azukibean]

Thanks, you're awesome! The algebra was a total pain.