chef99
- 75
- 4
Homework Statement
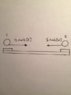
Two frictionless pucks are placed on a level surface, as shown(see diagram) at an initial distance of 20.0m. The mass of puck 1 is 0.80kg and has a charge of +3.0 x10-4 C, while puck two has a mass of 0.40 kg and a charge of +3.0 x10-4 C. The initial velocity of puck 1 is 12.0m/s [E]. The initial velocity of puck 2 is 8.0m/s [W]. Find the minimum distance between the two pucks.
Homework Equations
Eto= Etf
The Attempt at a Solution
Eto= Etf
Epo + Eko = Epf + Ekf
0 + Eko = Epf + 0
1/2 m(v1o)2 + 1/2 m(v2o)2 = kq1q1/r
1/2(0.80kg)(12.0m/s)2 + 1/2(0.40kg)(8.0m/s)2 = (9.0 x109)(3.0 x10-4)((3.0 x10-4) / r
70.4kgm/s = 810Nm / r
r = 810Nm / 70.4kgm/s
r = 11.5m
The minimum distance between the two puck will be 11.5m.
This is the first time I've tried to determine the minimum value of r (I have only determined the final velocity of the pucks) so I just tried what I thought made sense. I'm pretty sure I have the right idea but just want to make sure. Any input is greatly appreciated.